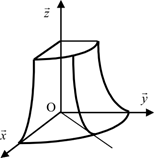
Tenseur d’inertie d’un solide de révolution
Si le solide homogène présente un axe de révolution alors tous les plans contenant cet axe sont des plans de symétrie. Le tenseur d’inertie, exprimé en un point \({\rm{O}}\) de l’axe de révolution \(\left( {{\rm{O}}\overrightarrow z } \right)\) et dans une base dont l’un des axes est l’axe de révolution, est de la forme :
\(\overline{\overline {{I_{{\rm{O,}}S}}}} = {\left[ {\begin{array}{*{20}{c}} A&0&0\\ 0&A&0\\ 0&0&C \end{array}} \right]_R}\)
car les plans \(\left( {{\rm{O}},\overrightarrow x ,\overrightarrow z } \right)\) et \(\left( {{\rm{O}},\overrightarrow y ,\overrightarrow z } \right)\) sont plans de symétrie donc :
\(\begin{array}{l} D{\rm{ = 0}} = \int_{{S_{y + }}} {yz{\kern 1pt} } {\kern 1pt} dm + \int_{{S_{y - }}} {yz} {\kern 1pt} dm = \int_{{S_{y + }}} {{\kern 1pt} \left( {y - y} \right)} {\kern 1pt} {\kern 1pt} z{\kern 1pt} dm\\ E = {\rm{0 = }}\int_{{S_{x + }}} {x{\kern 1pt} z{\kern 1pt} } {\kern 1pt} dm + \int_{{S_{x - }}} {x{\kern 1pt} z} {\kern 1pt} dm = \int_{{S_{x + }}} {{\kern 1pt} \left( {x - x} \right)} {\kern 1pt} {\kern 1pt} z{\kern 1pt} dm\\ F = {\rm{0}} = \int_{{S_{y + }}} {xy{\kern 1pt} } dm + \int_{{S_{y - }}} {xy} {\kern 1pt} dm = \int_{{S_{y + }}} {{\kern 1pt} x\left( {y - y} \right)} {\kern 1pt} {\kern 1pt} {\kern 1pt} dm \end{array}\)
et \(B = \int_S {\left( {{y^2} + {z^2}} \right)} {\kern 1pt} dm{\rm{ = }}\int_S {\left( {{x^2} + {z^2}} \right)} {\kern 1pt} dm = \int_S {\left( {{y^2} + {z^2}} \right)} {\kern 1pt} dm = A\)