Dynamique des systèmes mécaniques

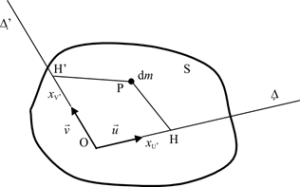
Connaissant le tenseur d’inertie \(\overline{\overline {{I_{{\rm{O}},S}}}}\) du solide \(S\) au point \(\rm{O}\) et dans la base \(R\left( {\overrightarrow x ,\overrightarrow y ,\overrightarrow z } \right),\) on peut déterminer le produit d’inertie par rapport à deux axes orthogonaux en \({\rm{O}}\), \(\Delta  = \left( {{\rm{O}}\overrightarrow u } \right)\) et \(\Delta ' = \left( {{\rm{O}}\overrightarrow v } \right),\) par le double produit suivant : \({I_{\Delta \Delta '}} =  - \overrightarrow u \,\overline{\overline {{I_{{\rm{O}},S}}}} \,\overrightarrow v\) ou \({I_{\Delta \Delta '}} =  - \overrightarrow v \,\overline{\overline {{I_{{\rm{O}},S}}}} \,\overrightarrow u\)