Transport du tenseur d’inertie
On peut calculer le tenseur d’inertie d’un solide en tout point (fixe par rapport au solide) à partir du tenseur d’inertie au centre d’inertie en utilisant le théorème de Koenig : \(\overline{\overline {{I_{{\rm{O,}}S}}}} {\rm{ = }}\overline{\overline {{I_{{\rm{G,}}S}}}} + \overline{\overline {{I_{{\rm{O,}}m}}}}\)
Le tenseur d’inertie au point \({\rm{O}}\) d’un solide est égal au tenseur d’inertie au centre d’inertie \({\rm{G}}\) du solide augmenté du tenseur d’inertie au point \({\rm{O}}\) de la masse totale du solide concentrée au centre d’inertie \({\rm{G}}.\)
Si le tenseur d’inertie au centre d’inertie \({\rm{G}}\) est \(\overline{\overline {{I_{{\rm{G}},S}}}} = {\left[ {\begin{array}{*{20}{r}} {{A^*}}&{ - {F^*}}&{ - {E^*}}\\ { - {F^*}}&{{B^*}}&{ - {D^*}}\\ { - {E^*}}&{ - {D^*}}&{{C^*}} \end{array}} \right]_R}\)
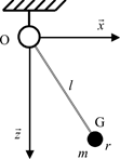
la masse du solide est \(m\) et la position du centre d’inertie \({\rm{G}}\) est définie par \(\overrightarrow {{\rm{OG}}} = a\overrightarrow x + b\overrightarrow y + c\overrightarrow z\)
Alors \(\overline{\overline {{I_{{\rm{O}},S}}}} = {\left[ {\begin{array}{*{20}{r}} A&{ - F}&{ - E}\\ { - F}&B&{ - D}\\ { - E}&{ - D}&C \end{array}} \right]_R}\) avec \(\begin{array}{l} A = {A^*} + m\left( {{b^2} + {c^2}} \right)\\ B = {B^*} + m\left( {{c^2} + {a^2}} \right)\\ C = {C^*} + m\left( {{a^2} + {b^2}} \right) \end{array}\) et \(\begin{array}{l} D = {D^*} + mbc\\ E = {E^*} + mca\\ F = {F^*} + mab \end{array}\)
\(\overline{\overline {{I_{{\rm{O}},S}}}} = \overline{\overline {{I_{{\rm{G,}}S}}}} + \overline{\overline {{I_{{\rm{O,}}m}}}} \quad \Leftrightarrow \quad {\left[ {\begin{array}{*{20}{r}} A&{ - F}&{ - E}\\ { - F}&B&{ - D}\\ { - E}&{ - D}&C \end{array}} \right]_R} = {\left[ {\begin{array}{*{20}{r}} {{A^*}}&{ - {F^*}}&{ - {E^*}}\\ { - {F^*}}&{{B^*}}&{ - {D^*}}\\ { - {E^*}}&{ - {D^*}}&{{C^*}} \end{array}} \right]_R} + m{\left[ {\begin{array}{*{20}{c}} {{b^2} + {c^2}}&{ - ab}&{ - ca}\\ { - ab}&{{c^2} + {a^2}}&{ - bc}\\ { - ca}&{ - bc}&{{a^2} + {b^2}}\end{array}} \right]_R}\)
Démonstration
\(\begin{array}{l} \overline{\overline {{{\rm{I}}_{{\rm{O,}}S}}}} \overrightarrow \Omega {\rm{ = }}\int_S {\overrightarrow {{\rm{OP}}} \wedge (\overrightarrow \Omega \wedge \overrightarrow {{\rm{OP}}} )} dm\\ = \int_S {{\rm{(}}\overrightarrow {{\rm{OG}}} {\rm{ + }}\overrightarrow {{\rm{GP}}} ) \wedge \left( {\overrightarrow \Omega \wedge {\rm{(}}\overrightarrow {{\rm{OG}}} {\rm{ + }}\overrightarrow {{\rm{GP}}} )} \right)} dm\\ = \int_S {\overrightarrow {{\rm{OG}}} \wedge (\overrightarrow \Omega \wedge \overrightarrow {{\rm{OG}}} } )dm + \int_S {\overrightarrow {{\rm{OG}}} \wedge (\overrightarrow \Omega \wedge \overrightarrow {{\rm{GP}}} } )dm + \int_S {\overrightarrow {{\rm{GP}}} \wedge (\overrightarrow \Omega \wedge \overrightarrow {{\rm{OG}}} )} dm + \int_S {\overrightarrow {{\rm{GP}}} \wedge (\overrightarrow \Omega \wedge \overrightarrow {{\rm{GP}}} )} dm\\ = \overrightarrow {{\rm{OG}}} \wedge (\overrightarrow \Omega \wedge \overrightarrow {{\rm{OG}}} )\int_S {dm} + \overrightarrow {{\rm{OG}}} \wedge (\overrightarrow \Omega \wedge \int_S {\overrightarrow {{\rm{GP}}} dm} ) + \int_S {\overrightarrow {{\rm{GP}}} dm \wedge (\overrightarrow \Omega \wedge \overrightarrow {{\rm{OG}}} )} + \overline{\overline {{{\rm{I}}_{{\rm{G,}}S}}}} \overrightarrow \Omega \\ = \overrightarrow {{\rm{OG}}} \wedge (\overrightarrow \Omega \wedge \overrightarrow {{\rm{OG}}} )m\quad \; + \overrightarrow {{\rm{OG}}} \wedge (\overrightarrow \Omega \wedge \overrightarrow 0 )\quad \quad \quad + \overrightarrow 0 \wedge (\overrightarrow \Omega \wedge \overrightarrow {{\rm{OG}}} )\quad \quad \quad + \overline{\overline {{{\rm{I}}_{{\rm{G,}}S}}}} \overrightarrow \Omega \\ = m\overrightarrow {{\rm{OG}}} \wedge (\overrightarrow \Omega \wedge \overrightarrow {{\rm{OG}}} ) + \overline{\overline {{{\rm{I}}_{{\rm{G,}}S}}}} \overrightarrow \Omega \\ = \overline{\overline {{I_{{\rm{O,}}m}}}} \overrightarrow \Omega + \overline{\overline {{I_{{\rm{G,}}S}}}} \overrightarrow \Omega \end{array}\)
Donc \(\overline{\overline {{I_{{\rm{O,}}S}}}} {\rm{ = }}\overline{\overline {{I_{{\rm{O,}}m}}}} + \overline{\overline {{I_{{\rm{G,}}S}}}}\)
Remarque :
Pour transporter le tenseur d’inertie d’un point à un autre, il faut obligatoirement passer par le centre d’inertie.
\(\overline{\overline {{I_{{\rm{A,}}S}}}}\) \(\quad \Rightarrow \quad\) \(\overline{\overline {{I_{{\rm{G,}}S}}}} = \overline{\overline {{I_{{\rm{A,}}S}}}} - \overline{\overline {{I_{{\rm{A,}}m}}}}\) \(\quad \Rightarrow \quad\) \(\overline{\overline {{I_{{\rm{B,}}S}}}} {\rm{ = }}\overline{\overline {{I_{{\rm{G,}}S}}}} + \overline{\overline {{I_{{\rm{B,}}m}}}}\)
Ce théorème de Koenig contient le théorème de Huygens :
Le moment d’inertie d’un solide par rapport à la droite \(\left( {{\rm{O}}\vec u} \right)\) est égal au moment d’inertie du solide par rapport à la droite \(\left( {{\rm{G}}\vec u} \right)\) augmenté du moment d’inertie de la masse du solide concentrée en \({\rm{G}}\) par rapport à la droite \(\left( {{\rm{O}}\vec u} \right)\).
En particulier : \(\begin{array}{l} A = {A^*} + m\left( {{b^2} + {c^2}} \right)\\ B = {B^*} + m\left( {{c^2} + {a^2}} \right)\\ C = {C^*} + m\left( {{a^2} + {b^2}} \right) \end{array}\)
Le produit d’inertie d’un solide par rapport à 2 droites perpendiculaires \(\left( {{\rm{O}}\vec u} \right)\) et \(\left( {{\rm{O}}\vec v} \right)\) est égal au produit d’inertie du solide par rapport aux droites \(\left( {{\rm{G}}\vec u} \right)\) et \(\left( {{\rm{G}}\vec v} \right)\) augmenté du produit d’inertie de la masse du solide concentrée en \({\rm{G}}\) par rapport aux droites \(\left( {{\rm{O}}\vec u} \right)\) et \(\left( {{\rm{O}}\vec v} \right)\).
En particulier : \(\begin{array}{l} D = {D^*} + mbc\\ E = {E^*} + mca\\ F = {F^*} + mab \end{array}\)
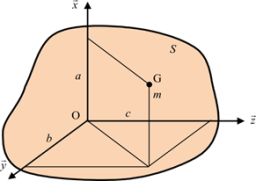
Pour deux axes parallèles dont l’un passe par le centre d’inertie \({\rm{G}},\) on a : \({I_\Delta } = {I_{{\Delta _{\rm{G}}}}} + m{d^{\rm{2}}}\)
Parmi tous les axes parallèles, le moment d’inertie est minimum par rapport à l’axe passant par centre d’inertie.
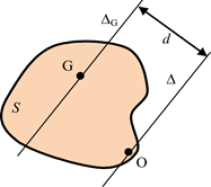
Exemple : Pendule simple
Le pendule est modélisé par une boule de rayon \(r.\)
\(\begin{array}{c} {I_{{\rm{O}}\vec y}} = {I_{{\rm{G}}\vec y}} + m{l^{\rm{2}}}\\ = \frac{2}{5}m{r^{\rm{2}}} + m{l^{\rm{2}}} \end{array}\)