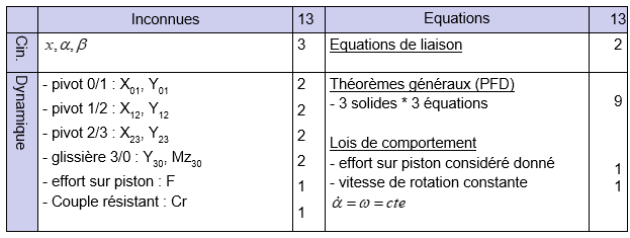
Appliquer le PFD – Utilisation de la méthode du système minimum
En fonction de l’objectif visé (connaître le mouvement ou déterminer une action de liaison), il n’est pas nécessaire d’écrire l’ensemble des équations. Si on s’intéresse seulement aux équations de mouvement (système d’équations différentielles permettant après résolution de connaître l’évolution de paramètres cinématiques au cours du temps à partir de conditions initiales) alors on cherchera à ne pas faire apparaître les actions de liaisons inconnues dans les équations.
Le système minimum est constitué du minimum d'équations nécessaires à écrire pour atteindre l’objectif : déterminer les équations régissant le mouvement du mécanisme.
La méthode consiste à choisir les équations des théorèmes généraux ne faisant pas apparaître les actions de liaison. Pour cela, on se servira du graphe de liaison : le principe consiste à isoler successivement différents sous-ensembles du système en ne coupant qu’une liaison paramétrée à la fois. On isolera alors l’ensemble des solides situés après la liaison coupée, autrement dit en bout de chaine cinématique (du coté où il n’y a pas le bâti). Parmi les 6 équations pouvant être écrites pour chaque isolement, on écrira seulement celles correspondant à une mobilité, ainsi aucune action de liaison n’interviendra dans l’équation.
Les seules actions de liaisons apparaissant dans les équations sont celles des liaisons non paramétrées. Ces actions seront déterminées grâce aux lois de comportement.
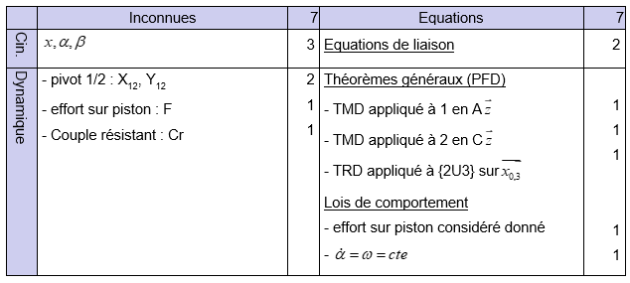
On dressera également un tableau bilan des équations et inconnues pour le système minimum :
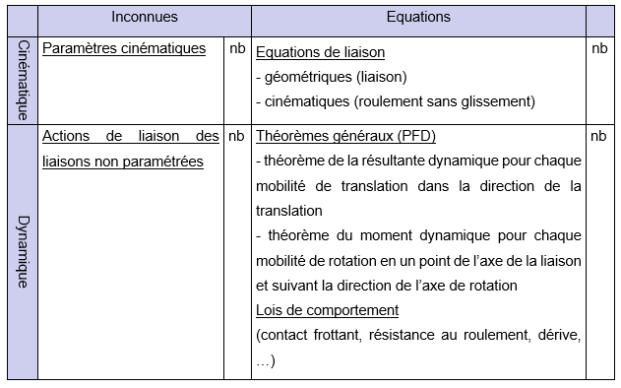
Exemple :
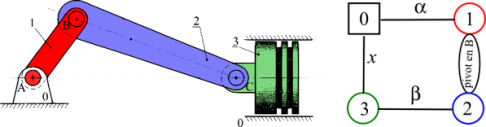
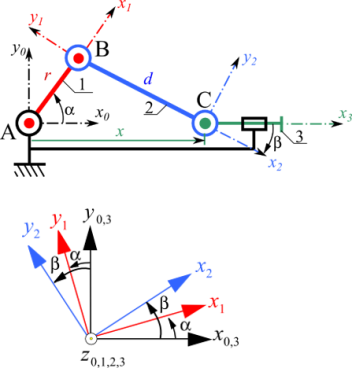
Equations remplaçant la liaison pivot en \(C\) :
\(\begin{array}{c} \overrightarrow {{{\rm{B}}_{{\rm{(1)}}}}{{\rm{B}}_{{\rm{(2)}}}}} = \overrightarrow 0 \\ = \overrightarrow {{{\rm{B}}_{{\rm{(1)}}}}{\rm{A}}} + \overrightarrow {{\rm{AC}}} + \overrightarrow {{\rm{C}}{{\rm{B}}_{{\rm{(2)}}}}} \\ = - r\overrightarrow {{x_1}} + x\overrightarrow {{x_0}} - d\overrightarrow {{x_2}} \end{array}\)
\(\begin{array}{l} \overrightarrow {{{\rm{B}}_{{\rm{(1)}}}}{{\rm{B}}_{{\rm{(2)}}}}} .\overrightarrow {{x_0}} = x - r\cos \alpha - d\cos \beta = 0\\ \overrightarrow {{{\rm{B}}_{{\rm{(1)}}}}{{\rm{B}}_{{\rm{(2)}}}}} .\overrightarrow {{y_0}} = - r\sin \alpha - d\sin \beta = 0 \end{array}\)
Mise en équation
TRD appliqué à {2U3} sur \(\overrightarrow {{x_{0,3}}}\)
\(\overrightarrow {{D_{3/0}}} = {m_{\rm{3}}}\overrightarrow {\Gamma ({{\rm{G}}_{\rm{3}}}/0)} = {m_{\rm{3}}}\ddot x\overrightarrow {{x_{0,3}}}\)
\(\overrightarrow {V({{\rm{G}}_{\rm{2}}}/0)} = \overrightarrow {V({\rm{C,}}2/0)} + \overrightarrow {{{\rm{G}}_{\rm{2}}}{\rm{C}}} \wedge \overrightarrow {{\Omega _{2/0}}} = \dot x\overrightarrow {{x_3}} + d/2\,\overrightarrow {{x_2}} \wedge \dot \beta \overrightarrow z = \dot x\overrightarrow {{x_3}} - \frac{{d\dot \beta }}{2}\,\overrightarrow {{y_2}}\)
\(\overrightarrow {\Gamma ({{\rm{G}}_{\rm{2}}}/0)} = {\left. {\frac{{d\overrightarrow {V({{\rm{G}}_{\rm{2}}}/0)} }}{{dt}}} \right|_0} = \ddot x\overrightarrow {{x_3}} - \frac{{d\ddot \beta }}{2}\,\overrightarrow {{y_2}} + \dot \beta \overrightarrow z \wedge - \frac{{d\dot \beta }}{2}\,\overrightarrow {{y_2}} = \ddot x\overrightarrow {{x_3}} - \frac{{d\ddot \beta }}{2}\,\overrightarrow {{y_2}} + \frac{{d{{\dot \beta }^2}}}{2}\,\overrightarrow {{x_2}}\)
\(\overrightarrow {{D_{2/0}}} = {m_2}\overrightarrow {\Gamma ({{\rm{G}}_{\rm{2}}}/0)} = {m_2}\left( {\ddot x\overrightarrow {{x_3}} - \frac{{d\ddot \beta }}{2}\,\overrightarrow {{y_2}} + \frac{{d{{\dot \beta }^2}}}{2}\,\overrightarrow {{x_2}} } \right)\)
\(\overrightarrow {\delta ({\rm{A,}}1/0)} = \frac{d}{{dt}}{\left( {\overrightarrow {\sigma ({\rm{A}},1/0)} } \right)_0} = \frac{d}{{dt}}{\left( {\overline{\overline {{I_{{\rm{A}},1}}}} \overrightarrow {{\Omega _{1/0}}} } \right)_0} = {C_1}\ddot \alpha \overrightarrow z\)
\(\overrightarrow {\delta ({{\rm{G}}_{\rm{2}}}{\rm{,}}2/0)} = \frac{d}{{dt}}{\left( {\overrightarrow {\sigma ({{\rm{G}}_{\rm{2}}},2/0)} } \right)_0} = \frac{d}{{dt}}{\left( {\overline{\overline {{I_{{{\rm{G}}_{\rm{2}}},2}}}} \overrightarrow {{\Omega _{2/0}}} } \right)_0} = {C_2}\ddot \beta \overrightarrow z\)
\(\begin{array}{*{20}{l}} {\overrightarrow {\delta ({\rm{C,}}2/0)} }&{ = \overrightarrow {\delta ({{\rm{G}}_{\rm{2}}}{\rm{,}}2/0)} + \overrightarrow {{\rm{C}}{{\rm{G}}_{\rm{2}}}} \wedge {m_2}\overrightarrow {\Gamma ({{\rm{G}}_{\rm{2}}}/0)} }\\ {}&\begin{array}{l} = {C_2}\ddot \beta \overrightarrow z - d/2\overrightarrow {{x_2}} \wedge {m_2}{\left( {\begin{array}{*{20}{c}} {\ddot x\cos \beta + d{{\dot \beta }^2}/2}\\ { - \ddot x\sin \beta - d\ddot \beta /2}\\ 0 \end{array}} \right)_2}\\ = \left( {{C_2}\ddot \beta + {m_2}\left( {\ddot x\sin \beta \,d/2 + {d^2}\ddot \beta /4} \right)} \right)\overrightarrow z \end{array} \end{array}\)
\(\overrightarrow {{R_{1 \to 2}}} = {X_{12}}\overrightarrow {{x_0}} + {Y_{12}}\overrightarrow {{y_0}}\)
\(\begin{array}{*{20}{c}} {\overrightarrow {{M_{1 \to 2}}({\rm{A}})} }&{ = \overrightarrow {{M_{1 \to 2}}({\rm{B}})} + \overrightarrow {{\rm{AB}}} \wedge \overrightarrow {{R_{1 \to 2}}} }\\ {}&\begin{array}{l} = \overrightarrow 0 + {\left( \begin{array}{l} r\cos \alpha \\ r\sin \alpha \\ 0 \end{array} \right)_0} \wedge {\left( \begin{array}{l} {X_{12}}\\ {Y_{12}}\\ 0 \end{array} \right)_0}\\ = \left( {{Y_{12}}r\cos \alpha - {X_{12}}r\sin \alpha } \right)\overrightarrow z \end{array} \end{array}\)
\(\begin{array}{*{20}{c}} {\overrightarrow {{M_{1 \to 2}}({\rm{C}})} }&{ = \overrightarrow {{M_{1 \to 2}}({\rm{B}})} + \overrightarrow {{\rm{CB}}} \wedge \overrightarrow {{R_{1 \to 2}}} }\\ {}&\begin{array}{l} = \overrightarrow 0 + {\left( \begin{array}{l} - d\cos \beta \\ - d\sin \beta \\ 0 \end{array} \right)_0} \wedge {\left( \begin{array}{l} {X_{12}}\\ {Y_{12}}\\ 0 \end{array} \right)_0}\\ = \left( { - d\cos \beta \;{Y_{12}} + d\sin \beta \;{X_{12}}} \right)\overrightarrow z \end{array} \end{array}\)
Bilan
\(\left\{ \begin{array}{l} \overrightarrow {{\rm{BB}}} .\overrightarrow {{x_0}} = 0\\ \overrightarrow {{\rm{BB}}} .\overrightarrow {{y_0}} = 0\\ \left( {\overrightarrow {{D_{{\rm{2/0}}}}} + \overrightarrow {{D_{{\rm{3/0}}}}} } \right).\overrightarrow {{x_0}} = \left( {\overrightarrow {{R_{1 \to 2}}} + \overrightarrow {{F_{gaz \to 3}}} } \right).\overrightarrow {{x_0}} \\ \overrightarrow {\delta ({\rm{A,}}1/0)} .\overrightarrow z = \left( {\overrightarrow {{M_{2 \to 1}}({\rm{A}})} + \overrightarrow {{M_{r \to 1}}({\rm{A}})} } \right).\overrightarrow z \\ \overrightarrow {\delta ({\rm{C,}}2/0)} .\overrightarrow z = \overrightarrow {{M_{1 \to 2}}({\rm{C}})} .\overrightarrow z \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x = r\cos \alpha + d\cos \beta \\ - r\sin \alpha = d\sin \beta \\ \left( {{m_3} + {m_2}} \right)\ddot x + {m_2}\left( {{{\dot \beta }^2}\cos \beta + \ddot \beta \sin \beta \,} \right)d/2 = {X_{12}} + {F_p}\\ {C_1}\ddot \alpha = {C_r} - \left( {{Y_{12}}r\cos \alpha - {X_{12}}r\sin \alpha } \right)\\ {C_2}\ddot \beta + {m_2}\left( {\ddot x\sin \beta \,d/2 + {d^2}\ddot \beta /4} \right) = - d\cos \beta \;{Y_{12}} + d\sin \beta \;{X_{12}} \end{array} \right.\)