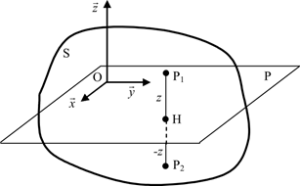
Tenseur d’inertie d’un solide ayant un plan de symétrie
Si un solide homogène possède un plan de symétrie alors les produits d’inertie relatifs à ce plan sont nuls.
Par exemple, si le plan \(\left( {{\rm{O}},\overrightarrow x ,\overrightarrow y } \right)\) est plan de symétrie du solide \(S\) alors le tenseur d’inertie de \(S\) en \({\rm{O}}\) exprimé dans la base \(R\left( {\overrightarrow x ,\overrightarrow y ,\overrightarrow z } \right)\) est de la forme :
\(\overline{\overline {{I_{{\rm{O,}}S}}}} = {\left[ {\begin{array}{*{20}{c}} A&{ - F}&0\\ { - F}&B&0\\ 0&0&C \end{array}} \right]_R}\)
car \(\begin{array}{l} D{\rm{ = }}\int_{{S_{z + }}} {y{\kern 1pt} z} dm + \int_{{S_{z - }}} {y{\kern 1pt} z} {\kern 1pt} dm = \int_{{S_{z + }}} {y{\kern 1pt} \left( {z - z} \right)} {\kern 1pt} dm{\rm{ = 0}}\\ E{\rm{ = }}\int_{{S_{z + }}} {x{\kern 1pt} z} {\kern 1pt} dm + \int_{{S_{z - }}} {x{\kern 1pt} z} {\kern 1pt} dm = \int_{{S_{z + }}} {x{\kern 1pt} \left( {z - z} \right)} {\kern 1pt} dm{\rm{ = 0}} \end{array}\)
L’axe \(\left( {{\rm{O}}\overrightarrow z } \right)\) est un axe principal d’inertie pour tout point \({\rm{O}}\) du plan de symétrie.