Moment d’inertie par rapport à un axe connaissant le tenseur en un point de l’axe
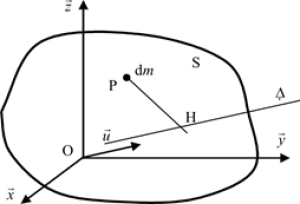
Connaissant le tenseur d’inertie \(\overline{\overline {{I_{{\rm{O}},S}}}}\) du solide \(S\) au point \({\rm{O}}\) et dans la base \(R\left( {\overrightarrow x ,\overrightarrow y ,\overrightarrow z } \right),\) on peut déterminer le moment d’inertie par rapport à l’axe \(\Delta = \left( {{\rm{O}}\overrightarrow u } \right)\) passant par \({\rm{O}}\) et de vecteur directeur \(\overrightarrow u\) par le double produit suivant : \({I_\Delta } = \overrightarrow u \,\overline{\overline {{I_{{\rm{O}},S}}}} \,\overrightarrow u\)
Démonstration
\(\begin{array}{l} {I_\Delta } = \int_S {{\rm{P}}{{\rm{H}}^2}dm} \quad > 0\\ = \int_S {{{\left( {\vec u \wedge \overrightarrow {{\rm{OP}}} } \right)}^2}dm} \\ = \int_S {\left( {\vec u \wedge \overrightarrow {{\rm{OP}}} } \right) \cdot \left( {\vec u \wedge \overrightarrow {{\rm{OP}}} } \right)dm} \\ = \vec u \cdot \int_S {\overrightarrow {{\rm{OP}}} \wedge \left( {\vec u \wedge \overrightarrow {{\rm{OP}}} } \right)dm} \\ = \vec u\,\overline{\overline {{I_{{\rm{O}},S}}}} \,\vec u \end{array}\)
Remarque :
On appelle rayon de giration par rapport à l’axe \(\Delta\), le scalaire \(R\) défini par : \({I_\Delta } = m{\kern 1pt} {r^2}\)
Exemple : Exemple général de calcul
Si \(\overline{\overline {{I_{{\rm{O}},S}}}} = {\left[ {\begin{array}{*{20}{r}} A&{ - F}&{ - E}\\ { - F}&B&{ - D}\\ { - E}&{ - D}&C \end{array}} \right]_R}\) et \(\overrightarrow u = {\left( \begin{array}{l} {u_x}\\ {u_y}\\ {u_z} \end{array} \right)_R}\) avec \(\left\| {\overrightarrow u } \right\| = 1\)
alors :
\(\begin{array}{*{20}{l}}{{I_\Delta }}&{ = \overrightarrow u \overline{\overline {{I_{{\rm{O}},S}}}} \overrightarrow u }\\{}&\begin{array}{l}= {\left( {{u_x}\;{u_y}\;{u_z}} \right)_R}{\left[ {\begin{array}{*{20}{c}}A&{ - F}&{ - E}\\{ - F}&B&{ - D}\\{ - E}&{ - D}&C\end{array}} \right]_R}{\left( \begin{array}{l}{u_x}\\{u_y}\\{u_z}\end{array} \right)_R}\\= {\left( {{u_x}\;{u_y}\;{u_z}} \right)_R}{\left( \begin{array}{l}A{u_x} - F{u_y} - E{u_z}\\F{u_x} + B{u_y} - D{u_z}\\E{u_x} - D{u_y} + C{u_z}\end{array} \right)_R}\\= {\left( {{u_x}\;{u_y}\;{u_z}} \right)_R}{\left( \begin{array}{l}A{u_x} - F{u_y} - E{u_z}\\F{u_x} + B{u_y} - D{u_z}\\E{u_x} - D{u_y} + C{u_z}\end{array} \right)_R}\\= A{u_x}^2 - F{u_y}{u_x} - E{u_z}{u_x} - F{u_x}{u_y} + B{u_y}^2 - D{u_z}{u_y} - E{u_x}{u_z} - D{u_y}{u_z} + C{u_z}^2\\= A{u_x}^2 + B{u_y}^2 + C{u_z}^2 - 2D{u_y}{u_z} - 2E{u_x}{u_z} - 2F{u_x}{u_y}\end{array}\end{array}\)