Linéaire annulaire ou sphère/cylindre ou sphère/prisme
Deux solides sont en liaison linéaire annulaire lorsque la zone de contact entre ces solides est constituée d’au moins 2 points de normales différentes.
Une liaison linéaire annulaire transmet un effort (ou une translation) dans le plan de la ligne de contact. Ce qui se traduit par projection sur un repère cartésien en deux composantes perpendiculaires.
Illustration d’une liaison linéaire annulaire
D’axe \(({\rm{O}}\overrightarrow x ).\)
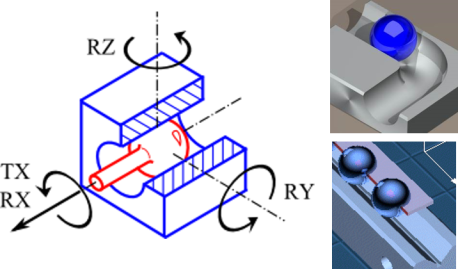
Schéma et torseurs associés à une liaison linéaire annulaire
D’axe \(({\rm{O}}\overrightarrow x ).\)
Torseur des actions transmissibles au centre de la liaison

\(\left\{ {{T_{i \to j}}} \right\} = {\left\{{\begin{array}{*{20}{c}} 0&0\\ {{F_y}}&0\\ {{F_z}}&0 \end{array}} \right\}_{{{\rm{R}}_{\rm{i}}}}}\)
Torseur cinématique au centre de la liaison
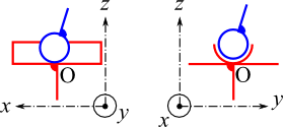
\(\left\{ {{V_{i/j}}} \right\} = {\left\{ {\begin{array}{*{20}{c}} {{\omega _x}}&{{V_x}{\rm{(O)}}}\\ {{\omega _y}}&0\\ {{\omega _z}}&0 \end{array}} \right\}_{{{\rm{R}}_{\rm{i}}}}}\)