Stabilisateur gyroscopique
Pour comprendre le fonctionnement d’un stabilisateur de roulis, on réalise le système expérimental représenté sur la figure 1 :
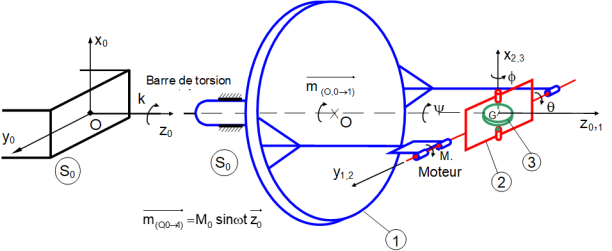
S1 est un corps en rotation autour d’un axe horizontal \((O,\ \overrightarrow{{{z}_{0,1}}})\) par rapport au référentiel S0.
Une barre de torsion équivalente à un ressort spiral est montée entre S0 et S1.
S2 est un cadre en liaison pivot d’axe \(\left( {{\rm{G}},\overrightarrow {{y_{1,2}}} } \right)\) avec le solide S1. Un moteur M1 est monté entre S1 et S2, son stator est relié à S1 et son rotor à S2.
S3 est un volant d’inertie en liaison pivot d’axe en liaison pivot d’axe \(\left( {{\rm{G}},\overrightarrow {{x_{2,3}}} } \right)\) avec le cadre S2. Un moteur M2 est monté entre S2 et S3.
Paramétrage
Un repère \({R_0}:({\rm{O}},\,\overrightarrow {{x_0}} ,\;\overrightarrow {{y_0}} ,\;\overrightarrow {{z_0}} )\) est lié au bâti S0, avec \(\overrightarrow {{x_0}}\) la direction verticale ascendante
Un repère \({R_1}:({\rm{G}},\,\overrightarrow {{x_1}} ,\;\overrightarrow {{y_1}} ,\;\overrightarrow {{z_1}} )\) est lié à S1 avec \({\rm{G}}\; \in \;({\rm{O}},\;\overrightarrow {{z_0}} )\)
Le paramètre du mouvement 1/0 est : \(\psi = (\overrightarrow {{x_0}} ,\;\overrightarrow {{x_1}} )\)
Un repère \({R_2}:(G,\,\overrightarrow {{x_2}} ,\;\overrightarrow {{y_2}} ,\;\overrightarrow {{z_2}} )\) est lié à S2
Le paramètre du mouvement 2/1 est : \(\theta = (\overrightarrow {{x_1}} ,\;\overrightarrow {{x_2}} )\)
Un repère \({R_3}:(G,\,\overrightarrow {{x_3}} ,\;\overrightarrow {{y_3}} ,\;\overrightarrow {{z_3}} )\) est lié à S3
Le paramètre du mouvement 3/2 est : \(\phi = (\overrightarrow {{y_2}} ,\;\overrightarrow {{y_3}} ), \overrightarrow {{y_3}}\) arbitraire
Données
Inertielles :
Le moment d’inertie de S1 par rapport à l'axe \(({\rm{O}},\;\overrightarrow {{z_0}} )\) est I. Son centre d’inertie est sur l’axe \(({\rm{O}},\;\overrightarrow {{z_{0,1}}} )\)
La masse de S2 et les éléments du tenseur en G sont négligeables
Le tenseur d’inertie de S3 est \(\overline{\overline{{{I}_{G,3}}}}={{\left[ \begin{array}{*{35}{l}} {{A}_{3}} & 0 & 0 \\ 0 & {{B}_{3}} & 0 \\ 0 & 0 & {{B}_{3}} \end{array} \right]}_{3,2}}.\) Son centre d'inertie est G
La raideur de la barre de torsion entre S0 et S1 est notée k
Un dispositif non représenté exerce entre (S0) et (S1) une action mécanique telle que :
\(\{ \overrightarrow {{F_{M0 \to 1}}} \; = \;\overrightarrow {0\;} ;\overrightarrow {{M_{M0 \to 1}}({\rm{G}})} \; = {M_0}\;\sin \;\omega \,t\;\overrightarrow {{z_0}} \}\)
Le moteur M1 monté entre (S1) et (S2) exerce une action telle que :
\(\{ \overrightarrow {{F_{M1 \to 2}}} \; = \;\overrightarrow {0\;} ;\overrightarrow {{M_{M1 \to 2}}({\rm{G}})} \; = {C_{m1}}\overrightarrow {{y_{1,2}}} \}\)
Le moteur M2 installé entre S2 et S3, entraîne le volant à vitesse constante \(\dot \phi = \;n = cte\) en exerçant une action telle que :
\(\{ \overrightarrow {{F_{M2 \to 3}}} \; = \;\overrightarrow {0\;} ;\overrightarrow {{M_{M2 \to 3}}({\rm{G}})} \; = {C_{m2}}\overrightarrow {{x_{2,3}}} \}\)
Hypothèses
\({{R}_{0}}:(O,\,\overrightarrow{{{x}_{0}}},\ \overrightarrow{{{y}_{0}}},\ \overrightarrow{{{z}_{0}}})\) est galiléen, \(\overrightarrow{{{x}_{0}}}\) verticale ascendante
Les liaisons sont supposées parfaites
Question
Ecrire les équations qui régissent le mouvement de S1 et S2.
Solution
Système minimum pour obtenir les équations du mouvement
TMD appliqué à {3} sur l’axe \((G,{\vec x_{2,3}})\) : \(\overrightarrow {\delta ({\rm{G}},3/0)} \,.\,\overrightarrow {{x_{2,3}}} = \overrightarrow {{M_{ext \to 3}}({\rm{G}})} \,.\,\overrightarrow {{x_{2,3}}}\)
Calcul du moment dynamique
\(\overrightarrow {\delta ({\rm{G}},3/0)} = {\left. {\frac{{d\,\overrightarrow {\sigma ({\rm{G}},3/0)} }}{{dt}}} \right)_0}\)
Avec : \(\overrightarrow {\sigma \,({\rm{G}},3/0)} = \overline{\overline {{I_{{\rm{G}},3}}}} \,\,\overrightarrow {\Omega {\,_{3/0}}} = {\left( {\begin{array}{*{20}{c}} {{A_{\,3}}}&0&0\\ 0&{{B_{\,3}}}&0\\ 0&0&{{B_{\,3}}} \end{array}} \right)_{3,2}}{\left( {\begin{array}{*{20}{c}} {\dot \phi - \dot \psi \sin \theta }\\{\dot \theta }\\ {\dot \psi \cos \theta } \end{array}} \right)_2} = {\left( {\begin{array}{*{20}{c}} {{A_{\,3}}\left( {\dot \phi - \dot \psi \sin \theta }\right)}\\ {{B_{\,3}}\,\dot \theta }\\ {{B_{\,3}}\,\dot \psi \cos \theta } \end{array}} \right)_2}\)
Soit : \(\overrightarrow {\delta ({\rm{G}},3/0)} = {\left( {\begin{array}{*{20}{c}} {{A_{\,3}}\left( {\ddot \phi - \ddot \psi \sin \theta - \dot \psi \,\dot \theta \cos \theta } \right)}\\ {{B_{\,3}}\,\ddot \theta }\\ {{B_{\,3}}\,\left( {\ddot \psi \cos \theta - \dot \psi \,\dot \theta {\mathop{\rm sins}\nolimits} \theta } \right)}\end{array}} \right)_2} + {\left( {\begin{array}{*{20}{c}} { - \dot \psi \sin \theta }\\ {\dot \theta }\\ {\dot \psi \cos \theta } \end{array}} \right)_2} \wedge {\left( {\begin{array}{*{20}{c}} {{A_{\,3}}\left( {\dot \phi - \dot \psi \sin \theta } \right)}\\ {{B_{\,3}}\,\dot \theta }\\ {{B_{\,3}}\,\dot \psi \cos \theta } \end{array}} \right)_2}\)
Soit : \(\overrightarrow {\delta ({\rm{G}},3/0)} = {\left( {\begin{array}{*{20}{c}}{{A_{\,3}}\left( {\ddot \phi - \ddot \psi \sin \theta - \dot \psi \,\dot \theta \cos \theta } \right)}\\ {{B_{\,3}}\,\ddot \theta + \left( {{B_{\,3}} - {A_{\,3}}} \right){{\dot \psi }^2}sin\theta \cos \theta + {A_{\,3}}\,\dot \phi \,\dot \psi \cos \theta }\\ {{B_{\,3}}\,\ddot \psi \cos \theta + \left( {{A_{\,3}} - 2{B_{\,3}}} \right)\dot \psi \,\dot \theta \sin \theta - {A_{\,3}}\,\dot \phi \dot \theta } \end{array}} \right)_2}\)
Bilan des Actions Mécaniques Extérieures sur {3}
Moteur M2 sur 3 : \(\overrightarrow {{M_{M2 \to 3}}({\rm{G}})} .\,\overrightarrow {{x_{\,2,3}}} = {C_{m2}}\)
Liaison 2/3 : \(\overrightarrow {{M_{2 \to 3}}({\rm{G}})} \,.\,\overrightarrow {{x_{\,2,3}}} = 0\)
Pesanteur sur 3 : \(\overrightarrow {{M_{pes \to 3}}({\rm{G}})} = \vec 0\)
L’équation est donc : \({A_{\,3}}\left( {\ddot \phi - \ddot \psi \sin \theta - \dot \psi \,\dot \theta \cos \theta } \right) = {C_{\,m2}}\)
TMD appliqué à {2;3} sur l’axe \(({\rm{G}},\overrightarrow {{y_{1,2}}} )\)
\((\overrightarrow {\delta ({\rm{G}},2/0)} + \overrightarrow {\delta ({\rm{G}},3/0)} )\,.\overrightarrow {{y_{1,2}}} = \overrightarrow {{M_{ext \to \{ 2;3\} }}(G)} \,.\,\overrightarrow {{y_{1,2}}}\)
Le moment dynamique du solide 2 est nul car sa masse négligeable. \(\overrightarrow {\delta ({\rm{G}},2/0)} \, = \vec 0\)
Bilan des Actions Mécaniques Extérieures sur {2;3}
Moteur M1 sur 2 : \(\overrightarrow {{M_{M1 \to 2}}({\rm{G}})} \,.\overrightarrow {{y_{1,2}}} = {C_{m1}}\)
Liaison 1/2 : \(\overrightarrow {{M_{1 \to 2}}({\rm{G}})} \,.\,\overrightarrow {{y_{1,2}}} = 0\)
Pesanteur sur 2 et 3 : \(\overrightarrow {{M_{pes \to 2}}({\rm{G}})} + \overrightarrow {{M_{pes \to 3}}({\rm{G}})} = \vec 0\)
L’équation est donc : \({B_{\,3}}\,\ddot \theta + \left( {{B_{\,3}} - {A_{\,3}}} \right){\dot \psi ^2}sin\theta \cos \theta + {A_{\,3}}\,\dot \phi \,\dot \psi \cos \theta = {C_{m1}}\,\)
TMD appliqué à {1;2;3} sur l’axe \(({\rm{G}},{\vec z_{0,1}})\)
\(\left( {\overrightarrow {\delta ({\rm{G}},1/0)} \, + \overrightarrow {\delta ({\rm{G}},2/0)} \, + \overrightarrow {\delta ({\rm{G}},3/0)} } \right)\,.\,\overrightarrow {{z_{0,1}}} = \overrightarrow {{M_{ext \to \left\{ {{\rm{1;2;3}}} \right\}}}({\rm{G}})} \,\,.\,\overrightarrow {{z_{0,1}}}\)
\(\overrightarrow {\delta ({\rm{G}},1/0)} \,.\,\overrightarrow {{z_{0,1}}} = {\left. {\frac{d}{{dt}}\overrightarrow {\sigma ({\rm{G}},1/0)} } \right|_0}\,.\,\overrightarrow {{z_{0,1}}} = {\left. {\frac{d}{{dt}}\overline{\overline {{I_{{\rm{G}},1}}}} \overrightarrow {{\Omega _{1/0}}} } \right|_0}\,.\,\overrightarrow {{z_{0,1}}} = I\,\ddot \psi\)
Car \({S_1}\) est en liaison pivot d’axe \(({\rm{G}},{\vec z_{0,1}})\) avec le galiléen \({S_0},\) donc le point G est fixe par rapport à 0.
Bilan des Actions Mécaniques Extérieures sur {1;2;3}
Excitation sur 1 : \(\overrightarrow {{M_{M0 \to 1}}({\rm{G}})} .\overrightarrow {{z_{0,1}}} = {M_0}\,\sin (\omega \,t)\)
Liaison 0/1 : \(\overrightarrow {{M_{0 \to 1}}({\rm{G}})} .\overrightarrow {{z_{0,1}}} = 0\)
Barre de torsion : \(\overrightarrow {{M_{bt \to 1}}({\rm{G}})} .\overrightarrow {{z_{0,1}}} = {M_{bt}} = - k\psi\)
Pesanteur sur 1, 2 et 3 : \(\left( {\overrightarrow {{M_{pes \to 1}}({\rm{G}})} + \overrightarrow {{M_{pes \to 2}}({\rm{G}})} + \overrightarrow {{M_{pes \to 3}}({\rm{G}})} } \right).\overrightarrow {{z_{0,1}}} = 0\)
Car \(\overrightarrow {{M_{pes \to 1}}({\rm{G}})} \, \bot \overrightarrow {\,{z_{0,1}}}\)
L’équation est :
\(I\,\ddot \psi - \left[ {{A_{\,3}}\left( {\ddot \phi - \ddot \psi \sin \theta - \dot \psi \,\dot \theta \cos \theta } \right)} \right]\sin \theta + \,\left[ {{B_{\,3}}\,\ddot \psi \cos \theta + \left( {{A_{\,3}} - 2{B_{\,3}}} \right)\dot \psi \,\dot \theta \sin \theta - {A_{\,3}}\,\dot \phi \,\dot \theta } \right]\,\cos \theta = {M_0}\,\sin (\omega \,t) - k\psi\)
On suppose, dans tout ce qui suit, que les angles \(\psi\) et \(\theta,\) ainsi que leur dérivée demeurent petits et que \(\left| n \right| > > \left| {\dot \psi } \right|\;\;\)et\(\;\;\left| n \right| > > \left| {\dot \theta } \right|\)
Question
Linéariser les équations dans l’état stationnaire \(\psi = 0, \theta = 0\) et \(\dot \phi = \eta = Cste.\)
Solution
On recherche un état stationnaire tel que \(\psi = {\psi _s} = Cste, \theta = {\theta _s} = Cste\) et \(\dot \phi = \eta = Cste.\)
Cette analyse est évidemment effectuée en l’absence de l’excitation extérieure \({M_0}\,\sin \left( {\omega \,t} \right).\)
On conclut alors : \({\psi _s} = 0\) et \({\theta _s} = Cste\) quelconque.
Dans la suite nous allons analyser le comportement au voisinage de la position stationnaire particulière où \({\theta _s} = 0.\)
En posant : \(\dot {\phi} = \eta = Cste, \psi = {\psi _s} + \bar \psi = \bar \psi\) et \(\theta = {\theta _s} + \bar \theta = \bar \theta\)
Avec : \(\bar \psi ,\,\,\dot {\bar \psi} ,\,\,\ddot {\bar \psi} ,\,\,\bar \theta ,\,\,\dot {\bar \theta} ,\,\,\ddot {\bar \theta}\) petits et du même ordre de grandeur.
Les 3 équations du mouvement deviennent par linéarisation :
\(\begin{array}{l} 0 = {C_{m2}}\\ {B_{\,3}}\,\ddot {\bar \theta} + {A_{\,3}}\,n\,\dot {\bar \psi} = {C_{m1}}\\ \left( {I + {B_{\,3}}} \right)\,\ddot {\bar \psi} - {A_{\,3}}\,n\,\dot {\bar \theta} \, = {M_0}\,\sin \left( {\omega \,t} \right) - k\bar \psi \end{array}\)
On suppose que le moteur M1 fournit un couple permettant d’asservir sa vitesse de rotation de sorte que \(\dot \theta = - p\;\dot \psi.\) Le sens de rotation est choisi de manière que : \(p\;n > 0.\)
Question
Montrer que le mouvement de S1 est régi par une équation de la forme :
\(\ddot \psi + 2\varepsilon {\omega _0}\;\dot \psi + \omega _0^2\;\psi = \frac{{{M_0}}}{{(I + {B_3})}}\;\sin \;\omega \,t\) en identifiant \({\omega _0}\) la pulsation propre et \(\varepsilon\) l’amortissement.
Solution
En remplaçant \(\dot {\theta } = - p\;\dot {\psi},\) on obtient : \((I + {B_{\,3}})\,\ddot {\bar \psi} + {A_{\,3}}{\kern 1pt} n\,p\,\dot {\bar \psi} + k\,\bar \psi = {M_0}\,\sin \left( {\omega \,t} \right)\)
Qui peut être mise sous la forme classique :
\(\,\ddot {\bar \psi} + 2\,\varepsilon \,{\omega _0}\,\dot {\bar \psi} + \omega _0^2\,\bar \psi = \frac{{{M_0}\,}}{{\left( {I + {B_{\,3}}} \right)}}\sin \left( {\omega \,t} \right)\) avec \(\omega _0^2\, = \frac{k}{{\left( {I + {B_{\,3}}} \right)}}\) et \(\varepsilon \, = \frac{{{A_{\,3}}\,\eta \,\rho }}{{2\,\sqrt {k\left( {I + {B_{\,3}}} \right)} }}\)
Question
Expliquer l’intérêt du gyroscope stabilisateur dans la réduction des oscillations.
Solution
La présence du gyroscope introduit de l’amortissement dans le système dynamique, permettant de diminuer l’amplitude de la réponse en régime permanent.
Question
A quelle condition le stabilisateur gyroscopique est-il efficace pour toutes les valeurs de \(\lambda \; = \frac{\omega }{{{\omega _0}}}\) ?
Solution
Cette réponse peut être obtenue directement en écrivant l’équation sous forme complexe :
\(\ddot{ \bar \psi} + 2\,\varepsilon \,{\omega _0}\,\dot{ \bar \psi} + \omega _0^2\,\bar \psi = \frac{{{M_0}\,}}{{\left( {I + {B_{\,3}}} \right)}}{e^{j\omega \,t}}\)
Où, avec complexe, est la réponse complexe associée à la réponse réelle \(\bar \psi (t) = {A_{\,\psi }}\,\sin \,(\omega \,t + \varphi ).\) En utilisant cette expression dans l’équation précédente il vient :
\(((\omega_0^2-\omega^2)+2j\epsilon \times\omega \times\omega_0)\underline{z}=\frac{M_0}{(I+B_3)}\)
Avec : \(A_{\psi}=|\underline{z}|=\frac{M_0}{(I+B_3)\sqrt{(\omega_0^2-\omega^2)^2+(2\epsilon \times\omega\times\omega_0)^2}}\)
Et : \(\phi=arg(\underline{z})\) telle que : \(tg(\varphi ) = \frac{{2\,\varepsilon \,\omega \,{\omega _0}}}{{\left( {{\omega ^2} - \omega _0^2} \right)}}\)
Il faut que \(|\underline{z}|<1.\)