Analyse du fonctionnement de l’équilibreuse
Le schéma ci-dessous représente le montage d’une roue S3 sur une équilibreuse S0
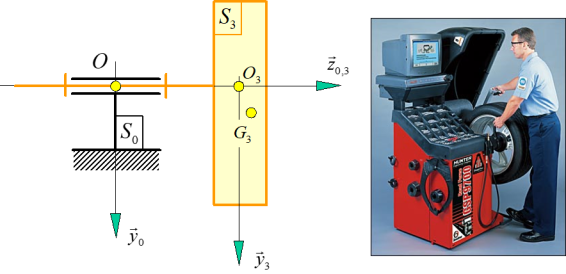
La roue S3 est en liaison pivot d’axe \(({{O}_{3}},\overrightarrow{{{z}_{0,3}}})\) avec l’équilibreuse S0, paramétrée \({{\theta }_{1}}=(\overrightarrow{{{x}_{0\,}}},\,\overrightarrow{{{x}_{3\,}}})\).
La roue S3 est de masse m3, de centre de masse G3 tel que \(\overrightarrow{{{O}_{3}} {{G}_{3}}}=b\,\overrightarrow{{{y}_{3}}}+c\,\overrightarrow{{{z}_{3}}}\) et de matrice d’inertie en O3 :
\(\overset{=}{\mathop{I}}\,({{O}_{3}},{{S}_{3}})={{\left( \begin{array}{*{35}{r}} {{A}_{\,3}} & -{{F}_{\,3}} & -{{E}_{\,3}} \\ -{{F}_{\,3}} & {{B}_{\,3}} & -{{D}_{\,3}} \\ -{{E}_{\,3}} & -{{D}_{\,3}} & {{C}_{\,3}} \\ \end{array} \right)}_{3}}\)
Un moteur, non représenté, exerce sur S3 un torseur couple \({{C}_{m}}\,\overrightarrow{{{z}_{0,3}}}\) tel que \(\dot{\theta }=\,\omega =cste\).
Question
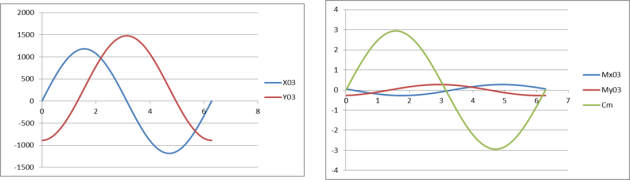
Déterminer et tracer les graphes d’évolution des actions mécaniques développées par la liaison 0/3.
Déterminer l’évolution de ces efforts lorsque la roue est équilibrée.
Indice
Pour simplifier les calculs on déterminera les éléments de réduction de ce torseur en O3.
Solution
Bilan des actions mécaniques extérieures s’exerçant sur le solide 3
Le couple moteur : \(\left\{ {{T_{moteur0 \to 3}}} \right\} = {\left\{ {\begin{array}{*{20}{c}} 0&0\\ 0&0\\ 0&{{C_m}} \end{array}} \right\}_0}\)
L’action de pesanteur : \({\left\{ {{T_{pesanteur \to 3}}} \right\}_{{{\rm{G}}_{\rm{3}}}}} = {\left\{ {\begin{array}{*{20}{c}} 0&0\\ {{m_3}g}&0\\ 0&0 \end{array}} \right\}_0}\) ou \({\left\{ {{T_{pesanteur \to 3}}} \right\}_{{{\rm{O}}_{\rm{3}}}}} = {\left\{ {\begin{array}{*{20}{c}} 0&{{m_3}gc}\\ {{m_3}g}&0\\ 0&{ - {m_3}gb\sin \theta } \end{array}} \right\}_0}\)
Car
\(\begin{array}{c} \overrightarrow {{M_{pes \to 3}}\left( {{{\rm{O}}_{\rm{3}}}} \right)} = \overrightarrow {{M_{pes \to 3}}\left( {{{\rm{G}}_{\rm{3}}}} \right)} + \overrightarrow {{{\rm{O}}_{\rm{3}}}{{\rm{G}}_{\rm{3}}}} \wedge {m_3}g\overrightarrow {{y_0}} \\ = {\left( \begin{array}{l} 0\\ 0\\ 0 \end{array} \right)_0} + {\left( \begin{array}{c} - b\sin \theta \\ b\cos \theta \\ c \end{array} \right)_0} \wedge {\left( \begin{array}{l} 0\\ {m_3}g\\ 0 \end{array} \right)_0} = {\left( \begin{array}{l} - {m_3}gc\\ 0\\ - {m_3}gb\sin \theta \end{array} \right)_0} \end{array}\)
avec \(\overrightarrow {{{\rm{O}}_{\rm{3}}}{{\rm{G}}_{\rm{3}}}} = b\overrightarrow {{y_3}} + c\overrightarrow {{z_3}} = - b\sin \theta \overrightarrow {{x_0}} + b\cos \theta \overrightarrow {{y_0}} + c\overrightarrow {{z_0}}\)
L’action de la liaison pivot entre le bâti (0) et la roue à équilibrer (3) : \({\left\{ {{T_{0 \to 3}}} \right\}_{{{\rm{O}}_{\rm{3}}}}} = {\left\{ {\begin{array}{*{20}{c}} {{X_{03}}}&{M{x_{03}}}\\ {{Y_{03}}}&{M{y_{03}}}\\ {{Z_{03}}}&0 \end{array}} \right\}_{{R_0}}}\)
En effet, le torseur a la même forme sur l’axe du pivot
\(\begin{array}{c} \overrightarrow {{M_{0 \to 3}}\left( {{{\rm{O}}_{\rm{3}}}} \right)} = \overrightarrow {{M_{pes \to 3}}\left( {\rm{O}} \right)} + \overrightarrow {{{\rm{O}}_{\rm{3}}}{\rm{O}}} \wedge \overrightarrow {{F_{0 \to 3}}} \\ = {\left( \begin{array}{c} Mx\\ My\\ 0 \end{array} \right)_{{R_0}}} + {\left( \begin{array}{c} 0\\ 0\\ d \end{array} \right)_{{R_0}}} \wedge {\left( \begin{array}{l} {X_{03}}\\ {Y_{03}}\\ {Z_{03}} \end{array} \right)_{{R_0}}} = {\left( \begin{array}{l} Mx - d\,{Y_{03}}\\ My + d\,{X_{03}}\\ 0 \end{array} \right)_{{R_0}}} = {\left( \begin{array}{l} M{x_{03}}\\ M{y_{03}}\\ 0 \end{array} \right)_{{R_0}}} \end{array}\)
Calcul de la résultante dynamique de la roue
\(\overrightarrow {{D_{3/0}}} = {m_3}\overrightarrow {\Gamma \left( {{{\rm{G}}_{\rm{3}}}/0} \right)}\) où \({{\rm{G}}_{\rm{3}}}\) le centre de masse de 3.
Par dérivation avec la base mobile :
\(\begin{array}{c} \overrightarrow {V\left( {{{\rm{G}}_{\rm{3}}}/0} \right)} = {\left[ {\frac{d}{{dt}}\overrightarrow {{{\rm{O}}_{\rm{3}}}{{\rm{G}}_{\rm{3}}}} } \right]_{{R_0}}} = {\left[ {\frac{d}{{dt}}\left( {b\overrightarrow {{y_3}} + c\overrightarrow {{z_3}} } \right)} \right]_{{R_0}}}\quad {\rm{car}}\;{{\rm{O}}_{\rm{3}}}\;{\rm{fixe}}\;{\rm{dans}}\;{R_0}\\ = {\left[ {\frac{d}{{dt}}\left( {b\overrightarrow {{y_3}} + c\overrightarrow {{z_3}} } \right)} \right]_{{R_0}}} + \,\overrightarrow {{\Omega _{3/0}}} \wedge \left( {b\overrightarrow {{y_3}} + c\overrightarrow {{z_3}} } \right)\\ = \dot \theta \overrightarrow z \wedge \left( {b\overrightarrow {{y_3}} + c\overrightarrow {{z_3}} } \right)\\ = - b\dot \theta \,\overrightarrow {{x_3}} \\ \\ \overrightarrow {\Gamma\left( {{{\rm{G}}_{\rm{3}}}/0} \right)} = {\left[ {\frac{d}{{dt}}\overrightarrow {V\left( {{{\rm{G}}_{\rm{3}}}/0} \right)} } \right]_{{R_0}}} = {\left[ {\frac{d}{{dt}}\left( { - b\dot \theta \,\overrightarrow {{x_3}} } \right)} \right]_{{R_0}}}\quad {\rm{car}}\; {{\rm{O}}_{\rm{3}}}\;{\rm{fixe}}\;{\rm{dans}}\;{R_0}\\ = - b\ddot \theta \,\overrightarrow {{x_3}} + \dot \theta \overrightarrow z \wedge - b\dot \theta \,\overrightarrow {{x_3}} \\ = - b\ddot \theta \,\overrightarrow {{x_3}} - b{{\dot \theta }^2}\,\overrightarrow {{y_3}} \end{array}\)
Si la roue est entrainée en rotation à vitesse constante \(\dot \theta = \omega = cte\) alors \(\ddot \theta = 0\).
Donc \({m_3}\overrightarrow {\Gamma \left( {{{\rm{G}}_{\rm{3}}}/0} \right)} = - {m_3}b{\omega ^2}\,\overrightarrow {{y_3}}.\)
Par formule du champ des accélérations :
\(\begin{array}{c} \overrightarrow {\Gamma ({{\rm{G}}_{\rm{3}}},3/0)} = \overrightarrow {\Gamma ({{\rm{O}}_{\rm{3}}},3/0)} + {\left( {\frac{{d\overrightarrow {{\Omega _{3/0}}} }}{{dt}}} \right)_{{R_3}}} \wedge \overrightarrow {{{\rm{O}}_{\rm{3}}}{{\rm{G}}_{\rm{3}}}} + \overrightarrow {{\Omega _{3/0}}} \wedge \left( {\overrightarrow {{\Omega _{3/0}}} \wedge \overrightarrow {{{\rm{O}}_{\rm{3}}}{{\rm{G}}_{\rm{3}}}} } \right)\\ = \overrightarrow 0 + {\left( {\begin{array}{*{20}{c}} 0\\ 0\\ {\ddot \theta } \end{array}} \right)_{{R_3}}} \wedge {\left( {\begin{array}{*{20}{c}} 0\\ b\\ c \end{array}} \right)_{{R_3}}} + {\left( {\begin{array}{*{20}{c}} 0\\ 0\\ {\dot \theta } \end{array}} \right)_{{R_3}}} \wedge {\left( {\begin{array}{*{20}{c}} 0\\ 0\\ {\dot \theta } \end{array}} \right)_{{R_3}}} \wedge {\left( {\begin{array}{*{20}{c}} 0\\ b\\ c \end{array}} \right)_{{R_3}}} = {\left( {\begin{array}{*{20}{c}} { - b\ddot \theta }\\ 0\\ 0 \end{array}} \right)_{{R_3}}} + {\left( {\begin{array}{*{20}{c}} 0\\ 0\\ {\dot \theta } \end{array}} \right)_{{R_3}}} \wedge {\left( {\begin{array}{*{20}{c}} { - b\dot \theta }\\ 0\\ 0 \end{array}} \right)_{{R_3}}}\\ = - b\ddot \theta \overrightarrow {{x_3}} - b\dot \theta \overrightarrow {{y_3}} \end{array}\)
\(\overrightarrow {\Gamma \left( {{{\rm{G}}_{\rm{3}}}/0} \right)} = b\left( { - \ddot \theta \cos \theta + {{\dot \theta }^2}\sin \theta } \right)\overrightarrow {{x_0}} - b\left( {\ddot \theta \sin \theta + b{{\dot \theta }^2}\cos \theta } \right)\overrightarrow {{y_0}}\)
Calcul du moment dynamique de la roue
En \({{\rm{O}}_{\rm{3}}}\) :
\(\begin{array}{c} \overrightarrow {\sigma \left( {{{\rm{O}}_{\rm{3}}}{\rm{,3}}/0} \right)} = \overline{\overline {{I_{{O_3},3}}}} \overrightarrow {{\Omega _{3/0}}} + m\overrightarrow {{{\rm{O}}_{\rm{3}}}{{\rm{G}}_{\rm{3}}}} \wedge \overrightarrow {V\left( {{{\rm{O}}_{\rm{3}}}{\rm{,3}}/0} \right)} \\ = {\left[ {\begin{array}{*{20}{c}} {{A_3}}&{ - {F_3}}&{ - {E_3}}\\ { - {F_3}}&{{B_3}}&{ - {D_3}}\\ { - {E_3}}&{ - {D_3}}&{{C_3}} \end{array}} \right]_3}{\left( {\begin{array}{*{20}{c}} 0\\ 0\\ {\dot \theta } \end{array}} \right)_3} + \overrightarrow 0 \quad {\rm{car}}\;{{\rm{O}}_{\rm{3}}}\;{\rm{fixe}}\;{\rm{dans}}\;{R_0}\\ = - {E_3}\dot \theta \overrightarrow {{x_3}} - {D_3}\dot \theta \overrightarrow {{y_3}} + {C_3}\dot \theta \overrightarrow {{z_3}} \end{array}\)
\(\begin{array}{c} \overrightarrow {\delta \left( {{{\rm{O}}_{\rm{3}}}{\rm{,3}}/0} \right)} = {\left[ {\frac{d}{{dt}}\overrightarrow {\sigma \left( {{{\rm{O}}_{\rm{3}}}{\rm{,3}}/0} \right)} } \right]_0} + \overrightarrow {V\left( {{{\rm{O}}_{\rm{3}}}/0} \right)} \wedge m\overrightarrow {V\left( {{{\rm{G}}_{\rm{3}}}/0} \right)} \\ = {\left[ {\frac{d}{{dt}}\overrightarrow {\sigma \left( {{{\rm{O}}_{\rm{3}}}{\rm{,3}}/0} \right)} } \right]_0}\quad {\rm{car}}\;{{\rm{O}}_{\rm{3}}}\;{\rm{fixe}}\;{\rm{dans}}\;{R_0}\\ = {\left( {\begin{array}{*{20}{c}} { - {E_3}\ddot \theta }\\ { - {D_3}\ddot \theta }\\ {{C_3}\ddot \theta } \end{array}} \right)_3} + {\left( {\begin{array}{*{20}{c}} 0\\ 0\\ {\dot \theta } \end{array}} \right)_3} \wedge {\left( {\begin{array}{*{20}{c}} { - {E_3}\dot \theta }\\ { - {D_3}\dot \theta }\\ {{C_3}\dot \theta } \end{array}} \right)_3}\\ = {\left( {\begin{array}{*{20}{c}} { - {E_3}\ddot \theta + {D_3}{{\dot \theta }^2}}\\ { - {D_3}\ddot \theta - {E_3}{{\dot \theta }^2}}\\ {{C_3}\ddot \theta } \end{array}} \right)_3} \end{array}\)
Si la roue est entrainée en rotation à vitesse constante \(\dot \theta = \omega = cte\) alors \(\ddot \theta = 0\).
Donc \(\overrightarrow {\delta \left( {{{\rm{O}}_{\rm{3}}}{\rm{,3}}/0} \right)} = {\left( {\begin{array}{*{20}{c}} {{D_3}{\omega ^2}}\\ { - {E_3}{\omega ^2}}\\ 0 \end{array}} \right)_3}\)
Conclusion
Quand la roue n’est pas équilibrée, les efforts dans la liaison varient sinusoïdalement.
Quand la roue est équilibrée, \(b = 0\), \({D_3} = 0\) et \({E_3} = 0\), les efforts dans la liaison sont constants et uniquement dus au poids. Ceci limite les vibrations et augmentent la durée de vie des pièces mécaniques telles que les roulements (phénomène de fatigue).
Application numérique :
Gravité : 9.81\(\mathrm{m.s^{−2}}\)
Rayon de la roue : 0.3 \(\mathrm{m}\)
Moment d’inertie de la roue : J = 0.5\(\mathrm{kg.m^2}\)