Exercice : Oscillation d’un cylindre sur un chemin circulaire [Dynamique]

Oscillation d’un cylindre sur un chemin circulaire

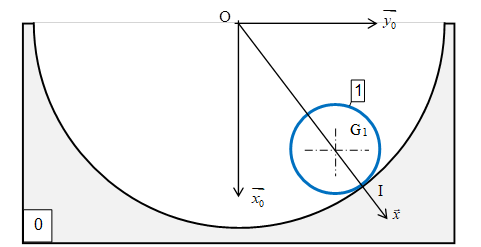
Un cylindre S₁ de révolution, plein homogène de rayon r et de masse m, peut rouler sans glisser dans un cylindre S₀, creux de rayon R. Les axes des deux cylindres sont horizontaux et parallèles.

Le mouvement de S₁/S₀ est défini par :

\(\phi =(\overrightarrow{{{x}_{0}}},\overrightarrow{x})\) paramétrant l’orientation du vecteur \(\overrightarrow{\text{O}{{\text{G}}_{1}}}\) par rapport à \(\overrightarrow{{{x}_{0}}}\)

\(\theta =(\overrightarrow{{{x}_{0}}},\overrightarrow{{{x}_{1}}})\) paramétrant la rotation propre de S₁ par rapport à S₀

Question

Ecrire l’équation traduisant le non-glissement entre S₁ et S₀ en \(\text{I}.\)

Solution

Tableau de bilan des inconnues et des équations

Inconnues		Equations
Cinématiques : \(\varphi,\) \(\theta\)	2	Roulement sans glissement en \({\rm{I}}\)	1
Dynamiques : contact ponctuel 01 imparfait : \({X_{01}},\) \({Y_{01}}\)	2	Principe fondamental de la dynamique appliqué au solide 1 (cas plan)	3
	4		4

Bilan des actions s’exerçant sur le cylindre (1) :

le poids \(\left\{ {{T_{poids \to 1}}} \right\} = \left\{ {\begin{array}{*{20}{c}} {\overrightarrow {{P_1}} = mg\overrightarrow {{x_0}} }\\ {\overrightarrow {{M_{{P_1}}}({G_1})} = \overrightarrow 0 } \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {\overrightarrow {{P_1}} = mg\cos \varphi \overrightarrow x - mg\sin \varphi \overrightarrow y }\\ {\overrightarrow {{M_{{P_1}}}({G_1})} = \overrightarrow 0 } \end{array}} \right\}\)

l’action de contact imparfait \(\left\{ {{T_{0 \to 1}}} \right\} = \left\{ {\begin{array}{*{20}{c}} {\overrightarrow {{F_{01}}} = {X_{01}}\overrightarrow x + {Y_{01}}\overrightarrow y }\\ {\overrightarrow {{M_{01}}({\rm{I}})} = \overrightarrow 0 } \end{array}} \right\}\)

\(\Rightarrow \left( {R - r} \right)\dot \varphi + r\dot \theta = 0\quad (4)\)

\(\begin{array}{c} \overrightarrow {V\left( {{{\rm{G}}_{\rm{1}}},1/0} \right)} = \overrightarrow {V\left( {{{\rm{G}}_{\rm{1}}}/0} \right)} = {\left. {\frac{{d\overrightarrow {{\rm{O}}{{\rm{G}}_{\rm{1}}}} }}{{dt}}} \right|_{{R_0}}} = \left( {R - r} \right){\left. {\frac{{d\overrightarrow x }}{{dt}}} \right|_{{R_0}}} = \left( {R - r} \right)\left( {{{\left. {\frac{{d\overrightarrow x }}{{dt}}} \right|}_R} + \overrightarrow {{\Omega _{R/{R_0}}}} \wedge \overrightarrow x } \right) = \left( {R - r} \right)\left( {0 + \dot \varphi \overrightarrow z \wedge \overrightarrow x } \right)\\ = \left( {R - r} \right)\dot \varphi \overrightarrow y \end{array}\)

Relation de roulement sans glissement

En \({\rm{I}}\) : \(\overrightarrow {V({\rm{I,1/0}})} = \overrightarrow 0\)

\(\begin{array}{c} \overrightarrow {V({\rm{I,1/0}})} = \overrightarrow {V({{\rm{G}}_1}{\rm{,1/0}})} + \overrightarrow {{\rm{I}}{{\rm{G}}_{\rm{1}}}} \wedge \overrightarrow {{\Omega _{1/0}}} \\ = \left( {R - r} \right)\dot \varphi \overrightarrow y - r\overrightarrow x \wedge \dot \theta \overrightarrow z \\ = \left( {\left( {R - r} \right)\dot \varphi + r\dot \theta } \right)\overrightarrow y \end{array}\)

\(\Rightarrow \left( {R - r} \right)\dot \varphi + r\dot \theta = 0\quad (4)\)

Question

Effectuer la mise en équations permettant d’étudier le mouvement de S₁/S₀.

Solution

Théorème de la résultante dynamique

\(\overrightarrow {{P_1}} + \overrightarrow {{F_{01}}} = m\overrightarrow {\Gamma ({{\rm{G}}_{\rm{1}}}/0)}\)

\(\overrightarrow {{\rm{O}}{{\rm{G}}_{\rm{1}}}} = \left( {R - r} \right)\overrightarrow x\)

\(\begin{array}{c} \overrightarrow {V\left( {{{\rm{G}}_{\rm{1}}}/0} \right)} = {\left. {\frac{{d\overrightarrow {{\rm{O}}{{\rm{G}}_{\rm{1}}}} }}{{dt}}} \right|_{{R_0}}} = \left( {R - r} \right){\left. {\frac{{d\overrightarrow x }}{{dt}}} \right|_{{R_0}}} = \left( {R - r} \right)\left( {{{\left. {\frac{{d\overrightarrow x }}{{dt}}} \right|}_R} + \overrightarrow {{\Omega _{R/{R_0}}}} \wedge \overrightarrow x } \right) = \left( {R - r} \right)\left( {0 + \dot \varphi \overrightarrow z \wedge \overrightarrow x } \right)\\ = \left( {R - r} \right)\dot \varphi \overrightarrow y \end{array}\) \(\begin{array}{c} \overrightarrow {\Gamma \left( {{{\rm{G}}_{\rm{1}}}/0} \right)} = \frac{d}{{dt}}\overrightarrow {V\left( {{{\rm{G}}_{\rm{1}}}/0} \right)} = \left( {R - r} \right){\left. {\frac{{d\dot \varphi \overrightarrow y }}{{dt}}} \right|_{{R_0}}} = \left( {R - r} \right)\left( {{{\left. {\frac{{d\dot \varphi \overrightarrow y }}{{dt}}} \right|}_R} + \overrightarrow {{\Omega _{R/{R_0}}}} \wedge \dot \varphi \overrightarrow y } \right) = \left( {R - r} \right)\left( {\ddot \varphi \overrightarrow y + \dot \varphi \overrightarrow z \wedge \dot \varphi \overrightarrow y } \right)\\ = \left( {R - r} \right)\left( {\ddot \varphi \overrightarrow y - {{\dot \varphi }^2}\overrightarrow x } \right) \end{array}\)

D’où \(\overrightarrow {{P_1}} + \overrightarrow {{F_{01}}} = m\overrightarrow {\Gamma ({{\rm{G}}_{\rm{1}}}/0)} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {mg\cos \varphi + {X_{01}} = - m\left( {R - r} \right){{\dot \varphi }^2}}\\ { - mg\sin \varphi + {Y_{01}} = m\left( {R - r} \right)\ddot \varphi } \end{array}} \right.\)

Théorème du moment dynamique en G1

\(\overrightarrow {{M_{{P_1}}}({{\rm{G}}_{\rm{1}}})} + \overrightarrow {{M_{01}}({{\rm{G}}_{\rm{1}}})} = \overrightarrow {\delta ({{\rm{G}}_{\rm{1}}},1/0)}\)

\(\overrightarrow {\delta ({{\rm{G}}_{\rm{1}}},1/0)} = \frac{d}{{dt}}\overrightarrow {\sigma ({{\rm{G}}_{\rm{1}}},1/0)}\)

avec \(\overrightarrow {\sigma ({{\rm{G}}_{\rm{1}}},1/0)} = \overline{\overline {{I_{{G_1},1}}}} .\overrightarrow {{\Omega _{1/0}}} = {\left[ {\begin{array}{*{20}{c}} {\frac{{m\left( {3{r^2} + {h^2}} \right)}}{{12}}}&0&0\\ 0&{\frac{{m\left( {3{r^2} + {h^2}} \right)}}{{12}}}&0\\ 0&0&{\frac{{m{r^2}}}{2}} \end{array}} \right]_R}{\left( {\begin{array}{*{20}{c}} 0\\ 0\\ {\dot \theta } \end{array}} \right)_R} = \frac{{m{r^2}}}{2}\dot \theta \overrightarrow z\)

donc \(\overrightarrow {\delta ({{\rm{G}}_{\rm{1}}},1/0)} = \frac{{m{r^2}}}{2}{\left. {\frac{{d\dot \theta \overrightarrow z }}{{dt}}} \right|_{{R_0}}} = \frac{{m{r^2}}}{2}\ddot \theta \overrightarrow z\)

par ailleurs \(\overrightarrow {{M_{01}}({{\rm{G}}_{\rm{1}}})} = \overrightarrow {{M_{01}}({\rm{I}})} + \overrightarrow {{{\rm{G}}_{\rm{1}}}{\rm{I}}} \wedge \overrightarrow {{F_{01}}} = \overrightarrow 0 + {\left( {\begin{array}{*{20}{c}} r\\ 0\\ 0 \end{array}} \right)_R} \wedge {\left( {\begin{array}{*{20}{c}} {{X_{01}}}\\ {{Y_{01}}}\\ 0 \end{array}} \right)_R} = r{Y_{01}}\overrightarrow z\)

d’où \(r{Y_{01}} = \frac{{m{r^2}}}{2}\ddot \theta\)

Question

Déterminer le coefficient de frottement minimal pour que l’hypothèse de non glissement soit vérifiée, dans le cas où le cylindre S₁est lâché d’une position initiale \(\phi (t=0)={{\phi }_{0}}\) avec une vitesse nulle \(\ \dot{\phi }(t=0)=0\).

Solution

Coefficient de frottement pour non glissement, avec les équations du TRD sur x et y et du TMD en G1 :

Pour que le roulement soit sans glissement, il faut que l’effort tangentiel \(T\) soit inférieur à l’effort normal \(N\) au contact multiplié le coefficient de frottement \(f\) : \(\left| T \right| < f.\left| N \right|\).

Ce qui se traduit ici par : \(\left| {{Y_{01}}} \right| < f.\left| {{X_{01}}} \right|\quad \Rightarrow \quad\) \(f > \frac{{\left| {{Y_{01}}} \right|}}{{\left| {{X_{01}}} \right|}}\)

On va alors chercher à exprimer \({Y_{01}}\) et \({X_{01}}\) en fonction de la position du solide 1 par rapport à 0.

On dispose pour cela de l’équation cinématique de roulement sans glissement et des équations de la dynamique.

On a les 4 équations suivantes : \(mg\cos \varphi + {X_{01}} = - m\left( {R - r} \right){\dot \varphi ^2}\) \(\left\{ {\begin{array}{*{20}{r}} {mg\cos \varphi + {X_{01}} = - m\left( {R - r} \right){{\dot \varphi }^2}}&{(1)}\\ { - mg\sin \varphi + {Y_{01}} = m\left( {R - r} \right)\ddot \varphi }&{(2)}\\ {r{Y_{01}} = \frac{{m{r^2}}}{2}\ddot \theta }&{(3)}\\ {\left( {R - r} \right)\dot \varphi + r\dot \theta = 0}&{(4)} \end{array}} \right.\)

D’après (2), \({Y_{01}} = m\left( {R - r} \right)\ddot \varphi + mg\sin \varphi\)

En dérivant (4), \(on a \left( {R - r} \right)\ddot \varphi = - r\ddot \theta\) et en la combinant avec (3) on obtient \(\left( {R - r} \right)\ddot \varphi = - \frac{2}{m}{Y_{01}}.\)

En remplaçant dans (2), on a \({Y_{01}} = - 2{Y_{01}} + mg\sin \varphi\) \(\Rightarrow {Y_{01}} = \frac{{mg\sin \varphi }}{3}\)

D’après (1), \({X_{01}} = - m\left( {R - r} \right){\dot \varphi ^2} - mg\cos \varphi\)

On cherche à tout exprimer en fonction de \(\varphi\). Pour cela, on intègre \(\ddot \varphi = - \frac{2}{{\left( {R - r} \right)m}}{Y_{01}} = - \frac{{2g}}{{3\left( {R - r} \right)}}\sin \varphi\), ce qui nous donne \(\frac{{{{\dot \varphi }^2}}}{2} = \frac{{2g}}{{3\left( {R - r} \right)}}\cos \varphi + cte\)

On détermine la constante d’intégration avec les conditions initiales \(\varphi (t = 0) = {\varphi _0}\) et \(\dot \varphi (t = 0) = 0\) :

\(cte = - \frac{{2g}}{{3\left( {R - r} \right)}}\cos {\varphi _0}\)

Donc en remplaçant dans l’expression de \({X_{01}}\) :

\({X_{01}} = - m\left( {R - r} \right)2\left( {\frac{{2g}}{{3\left( {R - r} \right)}}\cos \varphi - \frac{{2g}}{{3\left( {R - r} \right)}}\cos {\varphi _0}} \right) - mg\cos \varphi = - \frac{{4mg}}{3}\left( {\cos \varphi - \cos {\varphi _0}} \right) - mg\cos \varphi\)

Le coefficient de frottement doit donc être supérieur à la valeur suivante :

\(f > \frac{{\left| {{Y_{01}}} \right|}}{{\left| {{X_{01}}} \right|}} = \frac{{\left| {\frac{{\sin \varphi }}{3}} \right|}}{{\left| { - \frac{4}{3}\left( {\cos \varphi - \cos {\varphi _0}} \right) - \cos \varphi } \right|}}\)

A \(t = 0\), \(f > \frac{{\left| {{Y_{01}}} \right|}}{{\left| {{X_{01}}} \right|}} = \frac{{\left| {\tan {\varphi _0}} \right|}}{3}\)

\(0 < \varphi < {\varphi _0} < \frac{\pi }{2}\) \(\Rightarrow\) \(\begin{array}{l} \sin \varphi < \sin {\varphi _0}\\ \cos \varphi > \cos {\varphi _0} \end{array}\) \(\Rightarrow\) \(f > \frac{{\left| {\tan {\varphi _0}} \right|}}{3} > \frac{{\left| {\frac{{\sin \varphi }} {3}} \right|}}{{\left| { - \frac{4}{3}\left( {\cos \varphi - \cos {\varphi _0}} \right) - \cos \varphi } \right|}}\)

Question

Etudier les petits mouvements \(\bar{\phi }\) du cylindre autour de la position d’équilibre \({{\phi }_{e}}=0,\) pour les conditions initiales \(\phi (t=0)={{\phi }_{0}}\), \(\ \dot{\phi }(t=0)=0\).

Solution

On souhaite étudier les petits mouvements du solide 1 par rapport à 0 autour de la position d’équilibre \(\varphi = 0\).

On obtient alors l’équation différentielle régissant l’évolution du paramètre \(\varphi\) :

\(- \frac{3}{2}mr\left( {R - r} \right)\ddot \varphi = mgr\sin \varphi \quad \Rightarrow \quad - \frac{3}{2}\left( {R - r} \right)\ddot \varphi = g\sin \varphi\)

Si \(\varphi\) petit alors \(\sin \varphi \approx \varphi \quad \Rightarrow \quad \ddot \varphi + \frac{{2g}}{{3\left( {R - r} \right)}}\varphi = 0\)

C’est une équation différentielle du second ordre à coefficients constants de type \(\ddot \varphi + {\omega ^2}\varphi = 0\) dont les solutions sont de la forme \(\varphi \left( t \right) = A\cos \left( {\omega \,t + B} \right)\)

On détermine les constantes \(A\) et \(B\) à partir des conditions initiales, \(\varphi (t = 0) = {\varphi _0}\) et \(\dot \varphi (t = 0) = 0\) :

\(\dot \varphi \left( 0 \right) = - A\omega \sin \left( {\omega \,0 + B} \right) = 0 \Rightarrow \sin \left( B \right) = 0 \Rightarrow B = 0\left[ \pi \right]\)

\(\varphi \left( 0 \right) = A\cos \left( {\omega \,0 + 0} \right) = {\varphi _0} \Rightarrow A = {\varphi _0}\)

On a finalement \(\varphi \left( t \right) = {\varphi _0}\cos \left( {\omega \,t} \right)\)

Question

Appliquer le théorème de l’énergie cinétique au solide 1.

Solution

Calcul de l’énergie cinétique

L’énergie cinétique du cylindre est :

\(\begin{array}{c} {T_{1/0}} = \frac{1}{2}m{\overrightarrow {V({{\rm{G}}_1}/0)} ^2} + \frac{1}{2}\overrightarrow {{\Omega _{1/0}}} \overline{\overline {{I_{{{\rm{G}}_1},1}}}} \overrightarrow {{\Omega _{1/0}}} \\ = \frac{1}{2}m{\left( {\left( {R - r} \right)\dot \varphi \overrightarrow y } \right)^2} + \frac{1}{2}{\left( {\begin{array}{*{20}{c}} 0&0&{\dot \theta } \end{array}} \right)_{0,1}}{\left[ {\begin{array}{*{20}{c}} .\\ .\\ 0 \end{array}\begin{array}{*{20}{c}} .\\ .\\ 0 \end{array}\begin{array}{*{20}{c}} 0\\ 0\\ {\frac{{m{r^2}}}{2}} \end{array}} \right]_{0,1}}{\left( {\begin{array}{*{20}{c}} 0\\ 0\\ {\dot \theta } \end{array}} \right)_{0,1}}\\ = \frac{1}{2}m{\left( {R - r} \right)^2}{{\dot \varphi }^2} + \frac{1}{2}\frac{{m{r^2}}}{2}{{\dot \theta }^2} \end{array}\)

On a l’équation de liaison de roulement sans glissement : \(\left( {R - r} \right)\dot \varphi + r\dot \theta = 0\)

Donc \({T_{1/0}} = \frac{3}{4}m{\left( {R - r} \right)^2}{\dot \varphi ^2}\)

Calcul des puissances

Puissance développée par la pesanteur

\({P_{pes \to 1/0}} = mg\overrightarrow {{x_0}} .\overrightarrow {V({{\rm{G}}_1}/0)} = mg\overrightarrow {{x_0}} .\left( {R - r} \right)\dot \varphi \overrightarrow y = - \sin \varphi \,mg\left( {R - r} \right)\dot \varphi\)

Fonction de force de pesanteur : \({U_{pes}} = mg{x_{{\rm{0}}{{\rm{G}}_1}}} + cte = mg\left( {R - r} \right)\cos \varphi \, + cte\)

\({P_{pes \to 1/0}} = \frac{{d{U_{pes}}}}{{dt}} = - mg\left( {R - r} \right)\dot \varphi \sin \varphi \,\)

Puissance développée par le contact (roulement sans glissement) :

\({P_{0 \to 1/0}} = \overrightarrow {{F_{0 \to 1}}} .\overrightarrow {V({\rm{I,1}}/0)} + \overrightarrow {{M_{0 \to 1}}({\rm{I}})} .\overrightarrow {{\Omega _{1/0}}} = \overrightarrow {{F_{0 \to 1}}} .\overrightarrow 0 + \overrightarrow 0 .\overrightarrow {{\Omega _{1/0}}} = 0\)

Théorème de l’énergie cinétique

\(\frac{{d{T_{\Sigma /0}}}}{{dt}} = {P_{ext \to \Sigma /0}} + {P_{int}} \quad \Rightarrow \quad \frac{3}{2}m{\left( {R - r} \right)^2}\dot \varphi \ddot \varphi = - mg\left( {R - r} \right)\dot \varphi \sin \varphi \, \quad \Rightarrow \quad \frac{3}{2}\left( {R - r} \right)\ddot \varphi + g\sin \varphi \, = 0\)

Remarque :

Seules les actions dérivant de fonction de force travaillent, on peut donc écrire le théorème sous sa forme intégrée :

\({T_{\Sigma /0}} - {U_{pes}} = cte \quad \Rightarrow \quad \frac{3}{4}m{\left( {R - r} \right)^2}{\dot \varphi ^2} + mg\left( {R - r} \right)\cos \varphi \, = cte \quad \Rightarrow \quad \frac{3}{4}\left( {R - r} \right){\dot \varphi ^2} + g\cos \varphi \, = cte\)