Equilibrage
La figure ci-dessous représente une roue de véhicule automobile S3 sur laquelle ont été positionnées deux masses d’équilibrage m1 et m2. Ces masses d’équilibrage sont localisées sur la jante (rayon r) sur sa partie avant (masse m1) et arrière (masse m2) par les angles \(\phi _1\) et \(\phi _2\).
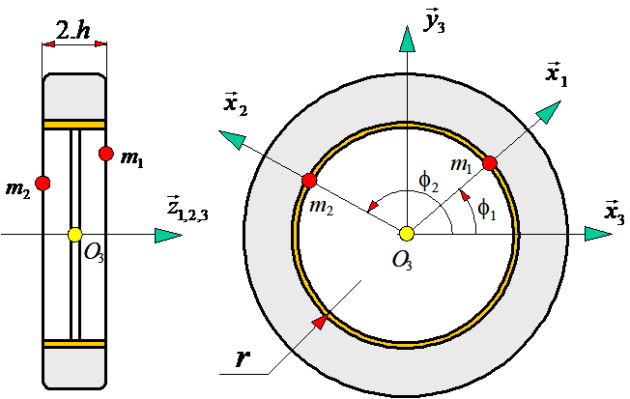
Géométrie des masses
masse m1 : masse ponctuelle telle que \(\overrightarrow{{{O}_{3}}{{G}_{1}}}={{(r,\ 0,\ h)}_{1}}\)
masse m2 : masse ponctuelle telle que \(\overrightarrow{{{O}_{3}}{{G}_{2}}}={{(r,\ 0,\ -h)}_{2}}\)
roue S3 non équilibrée : masse m3, centre de masse G3 tel que \(\overrightarrow{{{O}_{3}}{{G}_{3}}}={{(a,\ b,\ c)}_{3}}\) et matrice d’inertie en O3 :
\(\overset{=}{\mathop{I}}\,({{O}_{3}},{{S}_{3}})={{\left[ \begin{array}{*{35}{r}} {{A}_{\,3}} & -{{F}_{\,3}} & -{{E}_{\,3}} \\ -{{F}_{\,3}} & {{B}_{\,3}} & -{{D}_{\,3}} \\ -{{E}_{\,3}} & -{{D}_{\,3}} & {{C}_{\,3}} \\ \end{array} \right]}_{3}}\)
Question
Donner les équations traduisant la condition « d’équilibrage statique » de la roue.
Indice
Le centre de masse G’3 de l’ensemble S’3 = {S3+m1+m2} est sur l’axe \(({{O}_{3}},\overrightarrow{{{z}_{3}}})\).
Solution
On dit qu’un système est équilibré statiquement si le centre de masse \({\rm{G'}}_{\rm{3}}^{}\) de l’ensemble \(S'_3 = \left\{ {S_3^{} + {m_1} + {m_2}} \right\}\) est sur l’axe de rotation \(\left( {{{\rm{O}}_3},\overrightarrow {{z_3}} } \right)\). C’est-à-dire si \(\left\{ \begin{array}{l} \overrightarrow {{{\rm{O}}_{\rm{3}}}{\rm{G}}{{\rm{'}}_{\rm{3}}}} .\overrightarrow {{x_3}} = 0\\ \overrightarrow {{{\rm{O}}_{\rm{3}}}{\rm{G}}{{\rm{'}}_{\rm{3}}}} .\overrightarrow {{y_3}} = 0 \end{array} \right.\)
La position du centre d’inertie \({\rm{G'}}_{\rm{3}}\) de l’ensemble \(S'_3\) est défini par :
\(\overrightarrow {{{\rm{O}}_{\rm{3}}}{\rm{G}}{{\rm{'}}_{\rm{3}}}} = \frac{{{m_1}\overrightarrow {{{\rm{O}}_{\rm{3}}}{{\rm{G}}_{\rm{1}}}} + {m_2}\overrightarrow {{{\rm{O}}_{\rm{3}}}{{\rm{G}}_{\rm{2}}}} + {m_3}\overrightarrow {{{\rm{O}}_{\rm{3}}}{{\rm{G}}_{\rm{3}}}} }}{{{m_1} + {m_2} + {m_3}}}\)
avec \(\overrightarrow {{{\rm{O}}_{\rm{3}}}{{\rm{G}}_{\rm{3}}}} = {\left( {\begin{array}{*{20}{c}} a\\ b\\ c \end{array}} \right)_3},\) \(\overrightarrow {{{\rm{O}}_{\rm{3}}}{{\rm{G}}_{\rm{1}}}} = {\left( {\begin{array}{*{20}{c}} r\\ 0\\ h \end{array}} \right)_1}\) et \(\overrightarrow {{{\rm{O}}_{\rm{3}}}{{\rm{G}}_{\rm{2}}}} = {\left( {\begin{array}{*{20}{r}} r\\ 0\\ { - h} \end{array}} \right)_2}\)
Si le centre d’inertie \({\rm{G'}}_{\rm{3}}\) est sur l’axe \(\left( {{{\rm{O}}_3},\overrightarrow {{z_3}} } \right)\) alors ces coordonnées par rapport à \({{\rm{O}}_3}\) sont égales à 0 suivant \(\overrightarrow {{x_3}}\) et \(\overrightarrow {{y_3}}\) :
\(\left\{ \begin{array}{l} \overrightarrow {{{\rm{O}}_{\rm{3}}}{\rm{G}}{{\rm{'}}_{\rm{3}}}} .\overrightarrow {{x_3}} = 0\\ \overrightarrow {{{\rm{O}}_{\rm{3}}}{\rm{G}}{{\rm{'}}_{\rm{3}}}} .\overrightarrow {{y_3}} = 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{c} {m_1}r\cos {\varphi _1} + {m_2}r\cos {\varphi _2} + {m_3}a = 0\\ {m_1}r\sin {\varphi _1} + {m_2}r\sin {\varphi _2} + {m_3}b = 0 \end{array} \right.\)
Question
Donner les équations traduisant la condition « d’équilibrage dynamique » de la roue.
Indice
La direction \(({{O}_{3}},\overrightarrow{{{z}_{3}}})\) est direction principale d’inertie de l’ensemble S’3 = {S3+m1+m2}.
Solution
On dit qu’un système est équilibré dynamiquement si l’axe de rotation \(\left( {{{\rm{O}}_3},\overrightarrow {{z_3}} } \right)\) est direction principale d’inertie de l’ensemble \(S'_3 = \left\{ {S_3^{} + {m_1} + {m_2}} \right\}.\) C’est-à-dire \(\left\{ \begin{array}{c} D{'_3} = 0\\ E{'_3} = 0 \end{array} \right.\)
La matrice d’inertie de l’ensemble \(S'_3\) est la somme des matrices d’inertie des 3 solides qui le composent :
\(\overline{\overline {{I_{{{\rm{O}}_{\rm{3}}}{\rm{,}}3'}}}} = \overline{\overline {{I_{{{\rm{O}}_{\rm{3}}}{\rm{,1}}}}}} + \overline{\overline {{I_{{{\rm{O}}_{\rm{3}}}{\rm{,2}}}}}} + \overline{\overline {{I_{{{\rm{O}}_{\rm{3}}}{\rm{,3}}}}}}\)
Elles doivent être exprimées au même point (ici \({{\rm{O}}_3}\)) et dans la même base (ici \({R_3}\)).
\(\overline{\overline {{I_{{{\rm{O}}_3},3}}}} = {\left[ {\begin{array}{*{20}{c}} {{A_3}}&{ - {F_3}}&{ - {E_3}}\\ { - {F_3}}&{{B_3}}&{ - {D_3}}\\ { - {E_3}}&{ - {D_3}}&{{C_3}} \end{array}} \right]_3}\)
Par définition, le tenseur d’inertie d’un solide \(S\) en un point \({\rm{O}}\) dans une base \(R\) est :
\(\overline{\overline {{I_{{\rm{O}},S}}}} = {\left[ {\begin{array}{*{20}{c}} A&{ - F}&{ - E}\\ { - F}&B&{ - D}\\ { - E}&{ - D}&C \end{array}} \right]_R} = {\left[ {\begin{array}{*{20}{c}} {\int_S {{y^2} + {z^2}dm} }&{ - \int_S {xy\,dm} }&{ - \int_S {xz\,dm} }\\ { - \int_S {xy\,dm} }&{\int_S {{z^2} + {x^2}dm} }&{ - \int_S {yz\,dm} }\\ { - \int_S {xz\,dm} }&{ - \int_S {yz\,dm} }&{\int_S {{x^2} + {y^2}dm} } \end{array}} \right]_R}\)
Donc le tenseur d’inertie en \({{\rm{O}}_3}\) dans la base \({R_3}\) pour une masse ponctuelle \({m_1}\) concentrée en \({{\rm{G}}_1}\) sera :
\(\overline{\overline {{I_{{{\rm{O}}_{\rm{3}}},1}}}} = {\left[ {\begin{array}{*{20}{c}} {{A_1}}&{ - {F_1}}&{ - {E_1}}\\ { - {F_1}}&{{B_1}}&{ - {D_1}}\\ { - {E_1}}&{ - {D_1}}&{{C_1}} \end{array}} \right]_3} = {\left[ {\begin{array}{*{20}{c}} {{m_1}\left( {{r^2}{{\sin }^2}{\varphi _1} + {h^2}} \right)}&{ - {m_1}{r^2}\cos {\varphi _1}\sin {\varphi _1}}&{ - {m_1}hr\cos {\varphi _1}}\\ { - {m_1}{r^2}\cos {\varphi _1}\sin {\varphi _1}}&{{m_1}\left( {{r^2}{{\cos }^2}{\varphi _1} + {h^2}} \right)}&{ - {m_1}hr\sin {\varphi _1}}\\ { - {m_1}hr\cos {\varphi _1}}&{ - {m_1}hr\sin {\varphi _1}}&{{m_1}{r^2}} \end{array}} \right]_3}\)
car \(\begin{array}{l} x = \overrightarrow {{{\rm{O}}_{\rm{3}}}{{\rm{G}}_{\rm{1}}}} .\overrightarrow {{x_3}} = r\cos {\varphi _1}\\ y = \overrightarrow {{{\rm{O}}_{\rm{3}}}{{\rm{G}}_{\rm{1}}}} .\overrightarrow {{y_3}} = r\sin {\varphi _1}\\ z = \overrightarrow {{{\rm{O}}_{\rm{3}}}{{\rm{G}}_{\rm{1}}}} .\overrightarrow {{z_3}} = h \end{array}\)
De même pour la masse 2, on a :
\(\overline{\overline {{I_{{{\rm{O}}_{\rm{3}}},2}}}} = {\left[ {\begin{array}{*{20}{c}} {{m_2}\left( {{r^2}{{\sin }^2}{\varphi _2} + {h^2}} \right)}&{ - {m_2}{r^2}\cos {\varphi _2}\sin {\varphi _1}}&{{m_2}hr\cos {\varphi _2}}\\ { - {m_2}{r^2}\cos {\varphi _2}\sin {\varphi _2}}&{{m_2}\left( {{r^2}{{\cos }^2}{\varphi _2} + {h^2}} \right)}&{{m_2}hr\sin {\varphi _2}}\\ {{m_2}hr\cos {\varphi _2}}&{{m_2}hr\sin {\varphi _2}}&{{m_2}{r^2}} \end{array}} \right]_3}\) car \(\begin{array}{l} x = \overrightarrow {{{\rm{O}}_{\rm{3}}}{{\rm{G}}_{\rm{2}}}} .\overrightarrow {{x_3}} = r\cos {\varphi _2}\\ y = \overrightarrow {{{\rm{O}}_{\rm{3}}}{{\rm{G}}_{\rm{2}}}} .\overrightarrow {{y_3}} = r\sin {\varphi _2}\\ z = \overrightarrow {{{\rm{O}}_{\rm{3}}}{{\rm{G}}_{\rm{2}}}} .\overrightarrow {{z_3}} = - h \end{array}\)
On a finalement les deux relations suivantes :
\(\left\{ \begin{array}{c} D{'_3} = {D_1} + {D_2} + {D_3} = 0\\ E{'_3} = {E_1} + {E_2} + {E_3} = 0 \end{array} \right.\) \(\Leftrightarrow \left\{ \begin{array}{c} D{'_3} = {m_1}rh\sin {\varphi _1} - {m_2}rh\sin {\varphi _2} + {D_3} = 0\\ E{'_3} = {m_1}rh\cos {\varphi _1} - {m_2}rh\cos {\varphi _2} + {E_3} = 0 \end{array} \right.\)
Bilan
On a 4 équations qui permettent de déterminer les 4 inconnues que sont \({m_1}\), \({m_2}\), \({\varphi _1}\) et \({\varphi _2}\).
Remarque :
On pouvait aussi facilement exprimer les tenseur d’inertie dans les bases 1 et 2 puis calculer les produits d’inertie (\({D_1},{E_1},{D_2}\) et \({E_2}\)) par un changement de base.
\(\overline{\overline {{I_{{{\rm{O}}_{\rm{3}}}{\rm{,1}}}}}} = {\left[ {\begin{array}{*{20}{c}} {{m_1}{h^2}}&0&{ - {m_1}rh}\\ 0&{{m_1}\left( {{r^2} + {h^2}} \right)}&0\\ { - {m_1}rh}&0&{{m_1}{r^2}} \end{array}} \right]_1}\) | \(\overline{\overline {{I_{{{\rm{O}}_{\rm{3}}}{\rm{,2}}}}}} = {\left[ {\begin{array}{*{20}{c}} {{m_2}{h^2}}&0&{{m_2}rh}\\ 0&{{m_2}\left( {{r^2} + {h^2}} \right)}&0\\ {{m_2}rh}&0&{{m_2}{r^2}} \end{array}} \right]_2}\) |
\(\begin{array}{c} - {D_1} = {\overrightarrow {{y_3}} ^t}\,\overline{\overline {{I_{{O_3},1}}}} \,\overrightarrow {{z_3}} \\ = {\left( {\begin{array}{*{20}{c}} {\sin {\varphi _1}}&{\cos {\varphi _1}}&0 \end{array}} \right)_1}{\left[ {\begin{array}{*{20}{c}} {{m_1}{h^2}}&0&{ - {m_1}rh}\\ 0&{{m_1}\left( {{r^2} + {h^2}} \right)}&0\\ { - {m_1}rh}&0&{{m_1}{r^2}} \end{array}} \right]_1}{\left( {\begin{array}{*{20}{c}} 0\\ 0\\ 1 \end{array}} \right)_1}\\ = {\left( {\begin{array}{*{20}{c}} {\sin {\varphi _1}}&{\cos {\varphi _1}}&0 \end{array}} \right)_1}{\left( {\begin{array}{*{20}{c}} { - {m_1}rh}\\ 0\\ {{m_1}{r^2}} \end{array}} \right)_1}\\ = - {m_1}rh\sin {\varphi _1} \end{array}\) | \(\begin{array}{c} - {E_1} = {\overrightarrow {{x_3}} ^t}\,\overline{\overline {{I_{{O_3},1}}}} \,\overrightarrow {{z_3}} \\ = {\left( {\begin{array}{*{20}{c}} {\cos {\varphi _1}}&{ - \sin {\varphi _1}}&0 \end{array}} \right)_1}{\left( {\begin{array}{*{20}{c}} { -{m_1}rh}\\ 0\\ {{m_1}{r^2}} \end{array}} \right)_1}\\ = - {m_1}rh\cos {\varphi _1} \end{array}\) |
\(- {D_2} = {\overrightarrow {{y_3}} ^t}\,\overline{\overline {{I_{{O_3},2}}}} \,\overrightarrow {{z_3}} = {m_2}rh\sin {\varphi _2}\) | \(\begin{array}{c} - {E_2} = {\overrightarrow {{x_3}} ^t}\,\overline{\overline {{I_{{O_3},2}}}} \,\overrightarrow {{z_3}} \\ = {m_2}rh\cos {\varphi _2} \end{array}\) |