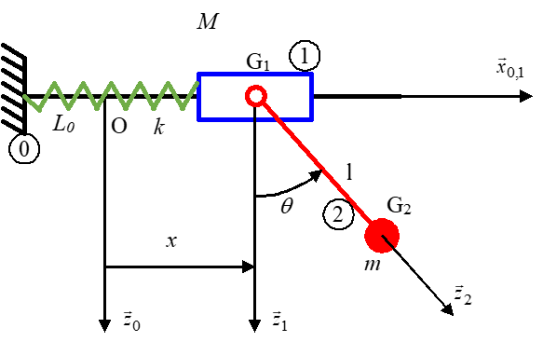
Pendule d'Euler
Le système est constitué :
d’un chariot (1) en liaison glissière de direction \(\overrightarrow {{x_0}},\) avec le bâti (0), de paramètre de translation \(x = \overrightarrow {{\rm{O}}{{\rm{G}}_{\rm{1}}}} .\overrightarrow {{x_0}}\)
d’un pendule (2) en liaison pivot d’axe \(({{\rm{G}}_{\rm{1}}},\overrightarrow {{y_1}} )\) avec le chariot (1), de paramètre de rotation \(\theta = (\overrightarrow {{z_{1,0}}} ,\;\overrightarrow {{z_2}} )\)
Le référentiel lié au bâti (0) est galiléen et \(\overrightarrow {{z_0}}\) est verticale descendante.
Le chariot (1) a une masse \(M\) et un moment d’inertie \({I_1}\) par rapport à l’axe \(({{\rm{G}}_{\rm{1}}},\overrightarrow {{y_0}} ).\)
Le pendule (2) a une masse \(m\) et un moment d’inertie \({I_2}\) par rapport à l’axe \(({{\rm{G}}_2},\overrightarrow {{y_0}} ).\)
Le chariot (1) est relié au bâti (0) par un ressort de raideur \(k\) dont l’action s’annule pour \(x = 0.\)
Question
Ecrire les équations du mouvement, à partir des théorèmes généraux.
Solution
Tableau bilan du système minimum pour obtenir les équations du mouvement
Inconnues | 2 | Equations | 2 |
Cinématiques x, q | 2 | De liaison | 0 |
Dynamiques | 0 | Théorèmes généraux TMD à 2 en \({{\rm{G}}_1}\overrightarrow {{y_1}}\) TRD à 1U2 sur \(\overrightarrow {{x_0}}\) | 1 1 |
Lois de comportement | 0 |
De manière à déterminer les équations régissant le mouvement (x, q) sans faire apparaitre les composantes d’action de liaisons, on écrit pour chaque liaison les équations du PFD suivant les composantes nulles du torseur en isolant l’ensemble des solides en bout de chaîne cinématique (c’est-à-dire après la liaison du côté où il n’y a pas le bâti). Ces deux équations sont :
le Théorème du Moment Dynamique appliqué au solide 2 en \({{\rm{G}}_1}\) suivant \(\overrightarrow {{y_1}}\)
le Théorème de la Résultante Dynamique appliqué à l’ensemble {1U2} suivant \(\overrightarrow {{x_0}}\)
\(\left\{ \begin{array}{l} {\rm{m}}{{\rm{l}}^{\rm{2}}}\ddot \theta + {\rm{ml}}\ddot x\cos \theta = - {\rm{mgl}}\sin \theta \\ {\rm{ml}}\ddot \theta \cos \theta - {\rm{ml}}{{\dot \theta }^2}\sin \theta + \left( {{\rm{M}} + {\rm{m}}} \right){\rm{\ddot x}} = - {\rm{K}}x - {\rm{b}}\dot x \end{array} \right.\)
Théorème de la résultante dynamique
Appliqué à 1+2 sur \(\overrightarrow {{x_0}}\)
Calcul de la résultante dynamique de {1+2} :
\(\overrightarrow {{D_{\left\{ {1 + 2} \right\}/0}}} = \overrightarrow {{D_{1/0}}} + \overrightarrow {{D_{2/0}}} = M\overrightarrow {\Gamma ({{\rm{G}}_{\rm{1}}}/0)} + m\overrightarrow {\Gamma ({{\rm{G}}_{\rm{2}}}/0)}\)
\(\overrightarrow {{\rm{O}}{{\rm{G}}_{\rm{1}}}} = x\overrightarrow {{x_{0,1}}} \Rightarrow \overrightarrow {V({{\rm{G}}_{\rm{1}}}/0)} = {\left. {\frac{{dx\overrightarrow {{x_{0,1}}} }}{{dt}}} \right|_0} = \dot x\overrightarrow {{x_{0,1}}} \Rightarrow \overrightarrow {\Gamma ({{\rm{G}}_{\rm{1}}}/0)} = {\left. {\frac{{d\overrightarrow {V({{\rm{G}}_{\rm{1}}}/0)} }}{{dt}}} \right|_0} = \ddot x\overrightarrow {{x_{0,1}}}\)
\(\Rightarrow \overrightarrow {{D_{1/0}}} = M\overrightarrow {\Gamma ({{\rm{G}}_{\rm{1}}}/0)} = M\,\ddot x\;\overrightarrow {{x_{0,1}}}\)
\(\begin{array}{c} \overrightarrow {V({{\rm{G}}_{\rm{2}}}/0)} = \overrightarrow {V({{\rm{G}}_{\rm{2}}},2/0)} \\ = \overrightarrow {V({{\rm{G}}_{\rm{1}}},2/0)} + \overrightarrow {{{\rm{G}}_{\rm{2}}}{{\rm{G}}_{\rm{1}}}} \wedge \overrightarrow {{\Omega _{2/0}}} \\ = \dot x\overrightarrow {{x_{0,1}}} + - L\overrightarrow {{z_2}} \wedge \dot \theta \overrightarrow y \\ = \dot x\overrightarrow {{x_{0,1}}} + L\dot \theta \overrightarrow {{x_2}} \end{array}\) ou \(\begin{array}{c} \overrightarrow {V({{\rm{G}}_{\rm{2}}}/0)} = {\left. {\frac{{d\overrightarrow {{\rm{O}}{{\rm{G}}_{\rm{2}}}} }}{{dt}}} \right|_0} = {\left. {\frac{{dx\overrightarrow {{x_{0,1}}} + L\,\overrightarrow {{z_2}} }}{{dt}}} \right|_0}\\ = \dot x\overrightarrow {{x_{0,1}}} + \overrightarrow 0 + \dot \theta \overrightarrow y \wedge L\overrightarrow {{z_2}} \\ = \dot x\overrightarrow {{x_{0,1}}} + L\dot \theta \overrightarrow {{x_2}} \end{array}\)
\(\overrightarrow {\Gamma ({{\rm{G}}_{\rm{2}}}/0)} = {\left. {\frac{{d\overrightarrow {V({{\rm{G}}_{\rm{2}}}/0)} }}{{dt}}} \right|_0} = \ddot x\overrightarrow {{x_{0,1}}} + L\ddot \theta \overrightarrow {{x_2}} - L{\dot \theta ^2}\overrightarrow {{z_2}}\)
\(\overrightarrow {{D_{2/0}}} = m\overrightarrow {\Gamma ({{\rm{G}}_{\rm{2}}}/0)} = m\ddot x\overrightarrow {{x_{0,1}}} + mL\ddot \theta \overrightarrow {{x_2}} - mL{\dot \theta ^2}\overrightarrow {{z_2}}\)
Bilan des actions mécaniques extérieures s’exerçant sur {1+2} :
action du ressort \(\overrightarrow {{F_{ressort0 \to 1}}} = - k\,x\,\overrightarrow {{x_{0,1}}}\)
action du poids \(\overrightarrow {{F_{pes \to 1}}} .\overrightarrow {{x_{0,1}}} + \overrightarrow {{F_{pes \to 2}}} .\overrightarrow {{x_{0,1}}} = 0\)
Donc le théorème de la résultante dynamique appliqué à 1+2 sur \(\overrightarrow {{x_0}}\) donne la relation suivante :
\(\begin{array}{c} \sum {\overrightarrow {{F_{ext \to \left\{ {1 + 2} \right\}}}} } .\overrightarrow {{x_{0,1}}} = \overrightarrow {{D_{\left\{ {1 + 2} \right\}/0}}} .\overrightarrow {{x_{0,1}}} \\ - kx = \left( {M + m} \right)\ddot x + mL\ddot \theta \cos \theta - mL{{\dot \theta }^2}\sin \theta \end{array}\)
Théorème du moment dynamique appliqué à 2
Sur \(\overrightarrow y\) en \({{\rm{G}}_{\rm{1}}}.\)
Calcul du moment dynamique de 2 :
\(\begin{array}{c} \overrightarrow {\delta ({{\rm{G}}_1},2/0)} = \overrightarrow {\delta ({{\rm{G}}_{\rm{2}}},2/0)} + \overrightarrow {{{\rm{G}}_{\rm{1}}}{{\rm{G}}_{\rm{2}}}} \wedge m\overrightarrow {\Gamma ({{\rm{G}}_{\rm{2}}},2/0)} \\ = {\left. {\frac{{d\overrightarrow {\sigma ({{\rm{G}}_{\rm{2}}},2/0)} }}{{dt}}} \right|_0} + \overrightarrow {{{\rm{G}}_{\rm{1}}}{{\rm{G}}_{\rm{2}}}} \wedge m\overrightarrow {\Gamma ({{\rm{G}}_{\rm{2}}},2/0)} \\ = {I_2}\ddot \theta \overrightarrow y + L\overrightarrow {{z_2}} \wedge m{\left( \begin{array}{l} \ddot x\cos \theta + L\ddot \theta \\ 0\\ \ddot x\sin \theta - L{{\dot \theta }^2} \end{array} \right)_2}\\ = {I_2}\ddot \theta \overrightarrow y + Lm\left( {\ddot x\cos \theta + L\ddot \theta } \right)\overrightarrow y \\ = \left[ {\left( {{I_2} + m{L^2}} \right)\ddot \theta + Lm\cos \theta \,\ddot x} \right]\overrightarrow y \end{array}\)
Bilan des actions mécaniques extérieures s’exerçant sur {1+2} :
action du poids \(\overrightarrow {{M_{pes \to 2}}({{\rm{G}}_1})} = \overrightarrow {{{\rm{G}}_1}{{\rm{G}}_2}} \wedge mg\overrightarrow {{z_0}} = {\left( \begin{array}{l} L\sin \theta \\ 0\\ L\cos \theta \end{array} \right)_0} \wedge {\left( \begin{array}{l} 0\\ 0\\ mg \end{array} \right)_0} = - mgL\sin \theta \overrightarrow y\)
action de 1 sur 2 par la liaison pivot \(\overrightarrow {{M_{1 \to 2}}({{\rm{G}}_1})} .\overrightarrow y = 0\)
Donc le théorème du moment dynamique appliqué à 2 sur \(\overrightarrow y\) en \({{\rm{G}}_{\rm{1}}}\) donne la relation suivante :
\(\begin{array}{c} \overrightarrow {\delta ({{\rm{G}}_1},2/0)} .\overrightarrow y = \sum {\overrightarrow {{M_{ext \to 2}}({{\rm{G}}_1})} } .\overrightarrow y \\ \left( {{I_2} + m{L^2}} \right)\ddot \theta + Lm\cos \theta \,\ddot x = - mgL\sin \theta \end{array}\)
Question
Linéariser les équations dans le cas où \(x\) et \(\theta\) sont petits.
Solution
Equations linéarisées
Linéarisation des équations autour de la position d’équilibre \(\left( {{x_e};{\theta _e}} \right) = \left( {0;0} \right)\)
Les paramètres cinématiques sont considérés comme la somme de la position d’équilibre et d’un petit mouvement (\(\bar x\) et \(\bar \theta\)) autour de la position d’équilibre, les vitesses et accélérations sont elles aussi petites :
\(x = {x_e} + \bar x = \bar x \Rightarrow \dot x = \dot{ \bar x} \Rightarrow \ddot x = \ddot{ \bar x}\)
\(\theta = {\theta _e} + \bar \theta = \bar \theta \Rightarrow \dot \theta = \dot{ \bar \theta} \Rightarrow \ddot \theta = \ddot{ \bar \theta}\)
Pour linéariser, on fait un développement limité à l’ordre 1 des fonctions (\(\cos \bar \theta \, \approx 1\) et \(\sin \bar \theta \, \approx \bar \theta\)) et les termes du second ordre (exemple : produit de 2 termes « petits ») sont négligés. Ceci se traduit ici par :
\(\left( {M + m} \right)\bar{ \ddot x} + Lm\bar{ \ddot \theta} + k\bar x = 0\)
\(mL\bar{ \ddot x} + \left( {m{L^2} + {I_2}} \right)\bar{ \ddot \theta} + mgL\bar \theta = 0\)
On peut également l’écrire sous la forme matricielle suivante :
\(\left[ {\begin{array}{*{20}{c}} {M + m}&{mL}\\ {mL}&{m{L^2} + {I_2}} \end{array}} \right]\left( \begin{array}{l} {\ddot{ \bar x}}\\ {\ddot{ \bar \theta} } \end{array} \right) + \left[ {\begin{array}{*{20}{c}} k&0\\ 0&{mgL} \end{array}} \right]\left( \begin{array}{l} {\bar x}\\ {\bar \theta } \end{array} \right) = \left( \begin{array}{l} 0\\ 0 \end{array} \right)\)
Question
Résoudre le système différentiel dans le cas où \(\frac{k}{{M + m}} = \frac{g}{l}\), \(M = 3\;m\) et \({I_2} \ll m{\ell ^2}\)
En cherchant directement la solution,
En utilisant les paramètres normaux.
On considère les conditions initiales suivantes à \(t = 0\), \(\left\{ \begin{array}{l} x = 0,\;\dot x = 0\\ \theta = {\theta _0},\;\dot \theta = 0 \end{array} \right.\)
Solution
En introduisant les relations \(\frac{k}{{M + m}} = \frac{g}{l}\), \(M = 3\;m\) et \({I_2} < < m{\ell ^2}\) :
\(\left\{ \begin{array}{l} \bar {\ddot x} + \frac{\ell }{4}\bar {\ddot \theta} + \frac{g}{\ell }\bar x = 0\\ \bar {\ddot x} + \ell \bar {\ddot \theta} + g\bar \theta = 0 \end{array} \right.\)
Méthode : Méthode directe (étant donné que la position d’équilibre est stable)
On cherche des solutions de la forme :
\(x = A{e^{j\omega t}}\) et \(\theta = B{e^{j\omega t}}\) ou \(x = A\cos (\omega t + {\varphi _a})\) et \(\theta = B\cos (\omega t + {\varphi _b})\)
Les équations deviennent alors :
\(\left\{ \begin{array}{l} - A{\omega ^2} - \frac{\ell }{4}B{\omega ^2} + \frac{g}{\ell }A = 0\\ - A{\omega ^2} - \ell B{\omega ^2} + gB = 0 \end{array} \right.\)
Ce qui constitue un système d’équations linéaires homogènes dont les inconnues sont A et B. Ce système admet une solution non identiquement nulle seulement si le déterminant est égal à zéro.
\(\begin{array}{l} \left\{ \begin{array}{l} (\frac{g}{\ell } - {\omega ^2})A - \frac{\ell }{4}{\omega ^2}B = 0\\ - {\omega ^2}A + (g - \ell {\omega ^2})B = 0 \end{array} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {\frac{g}{\ell } - {\omega ^2}}&{ - \frac{\ell }{4}{\omega ^2}}\\ { - {\omega ^2}}&{g - \ell {\omega ^2}} \end{array}} \right]\left( \begin{array}{l} A\\ B \end{array} \right) = \left( \begin{array}{l} 0\\ 0 \end{array} \right)\\ \det = (\frac{g}{\ell } - {\omega ^2})(g - \ell {\omega ^2}) - \frac{\ell }{4}{\omega ^4} = \frac{{{g^2}}}{\ell } - 2g{\omega ^2} + \ell {\omega ^4} - \frac{\ell }{4}{\omega ^4} = \frac{{3\ell }}{4}{\omega ^4} - 2g{\omega ^2} + \frac{{{g^2}}}{\ell } = 0 \end{array}\)
Les solutions d’une équation du second degré du type \(a{r^2} + br + c = 0\) sont :
si \(\Delta = {b^2} - 4ac > 0\) : \({r_1} = \frac{{ - b - \sqrt \Delta }}{{2a}}\) et \({r_2} = \frac{{ - b + \sqrt \Delta }}{{2a}}\)
si \(\Delta = {b^2} - 4ac = 0\) : \({r_1} = {r_2} = \frac{{ - b}}{{2a}}\)
si \(\Delta = {b^2} - 4ac < 0\) : \({r_1} = \frac{{ - b - i\sqrt {\left| \Delta \right|} }}{{2a}}\) et \({r_2} = \frac{{ - b + i\sqrt {\left| \Delta \right|} }}{{2a}}\)
Dans notre cas, on a \(\Delta = 4{g^2} - 4\frac{3}{4}\ell \frac{{{g^2}}}{\ell } = {g^2} > 0\)
Donc 2 racines réelles : \({\omega _1}^2 = \frac{{2g - g}}{2}\frac{4}{{3\ell }} = \frac{{2g}}{{3\ell }}\) et \({\omega _2}^2 = \frac{{2g + g}}{2}\frac{4}{{3\ell }} = \frac{{2g}}{\ell }\)
Les solutions sont donc :
\(\begin{array}{l} x = {A_1}\cos ({\omega _1}t + {\varphi _{a1}}) + {A_2}\cos ({\omega _2}t + {\varphi _{a2}})\\ \theta = {B_1}\cos ({\omega _1}t + {\varphi _{b1}}) + {B_2}\cos ({\omega _2}t + {\varphi _{b2}}) \end{array}\)
Méthode : Méthode avec les paramètres normaux (base propre)
\(\left[ {\begin{array}{*{20}{c}} 1&{\ell /4}\\ 1&\ell \end{array}} \right]\left( \begin{array}{l} {\ddot {\bar x}}\\ {\ddot {\bar \theta}} \end{array} \right) + \left[ {\begin{array}{*{20}{c}} {g/\ell }&0\\ 0&g \end{array}} \right]\left( \begin{array}{l} {\bar x}\\ {\bar \theta } \end{array} \right) = \left( \begin{array}{l} 0\\ 0 \end{array} \right)\)
Recherche des valeurs propres :
\(\begin{array}{l} \left( \begin{array}{l} {\ddot {\bar x}}\\ {\ddot {\bar \theta}} \end{array} \right) + \frac{1}{{\ell - \ell /4}}\left[ {\begin{array}{*{20}{c}} \ell &{ - \ell /4}\\ { - 1}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {g/\ell }&0\\ 0&g \end{array}} \right]\left( \begin{array}{l} {\bar x}\\ {\bar \theta } \end{array} \right) = \left( \begin{array}{l} 0\\ 0 \end{array} \right)\\ \left( \begin{array}{l} {\ddot {\bar x}}\\ {\ddot {\bar \theta}} \end{array} \right) + \frac{4}{{3\ell }}\left[ {\begin{array}{*{20}{c}} g&{ - g\ell /4}\\ { - g/\ell }&g \end{array}} \right]\left( \begin{array}{l} {\bar x}\\ {\bar \theta } \end{array} \right) = \left( \begin{array}{l} 0\\ 0 \end{array} \right) \end{array}\)
\(\begin{array}{l} \det (\left[ {\begin{array}{*{20}{c}} {g - \lambda }&{ - g\ell /4}\\ { - g/\ell }&{g - \lambda } \end{array}} \right]) = {(g - \lambda )^2} - \frac{{{g^2}}}{4} = {g^2} - 2g\lambda + {\lambda ^2} - \frac{{{g^2}}}{4} = {\lambda ^2} - 2g\lambda + \frac{{3{g^2}}}{4} = 0\\ \Delta = 4{g^2} - 3{g^2} = {g^2}\\ {\lambda _1} = \frac{4}{{3\ell }}\frac{{2g - g}}{2} = \frac{4}{{3\ell }}\frac{g}{2} = \frac{{2g}}{{3\ell }} = \omega _1^2\\ {\lambda _2} = \frac{4}{{3\ell }}\frac{{2g + g}}{2} = \frac{4}{{3\ell }}\frac{{3g}}{2} = \frac{{2g}}{\ell } = \omega _2^2 \end{array}\)
Recherche des vecteurs propres :
\(\begin{array}{l} \left( {\frac{4}{{3\ell }}\left[ {\begin{array}{*{20}{c}} g&{ - g\ell /4}\\ { - g/\ell }&g \end{array}} \right] - {\lambda _1}\left[ {\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right]} \right)\left( \begin{array}{l} {\alpha _{11}}\\ {\alpha _{21}} \end{array} \right) = \left( \begin{array}{l} 0\\ 0 \end{array} \right)\\ \left( {\frac{4}{{3\ell }}\left[ {\begin{array}{*{20}{c}} {g/2}&{ - g\ell /4}\\ { - g/\ell }&{g/2} \end{array}} \right]} \right)\left( \begin{array}{l} {\alpha _{11}}\\ {\alpha _{21}} \end{array} \right) = \left( \begin{array}{l} 0\\ 0 \end{array} \right)\\ \left\{ \begin{array}{l} \frac{g}{2}{\alpha _{11}} - \frac{{g\ell }}{4}{\alpha _{21}} = 0\\ - \frac{g}{\ell }{\alpha _{11}} + \frac{g}{2}{\alpha _{21}} = 0 \end{array} \right. \Rightarrow \left\{ \begin{array}{l} \frac{g}{2}{\alpha _{11}} - \frac{{g\ell }}{4}{\alpha _{21}} = 0\\ {\alpha _{21}} = \frac{2}{\ell }{\alpha _{11}} \end{array} \right. \Rightarrow \left\{ \begin{array}{l} \frac{g}{2}{\alpha _{11}} - \frac{g}{2} {\alpha _{11}} = 0\\ {\alpha _{21}} = \frac{2}{\ell }{\alpha _{11}} \end{array} \right. \end{array}\)
Donc le 1er vecteur propre est \(\overrightarrow {{W_1}} = {\alpha _{11}}\left( \begin{array}{l} 1\\ \frac{\ell }{2} \end{array} \right)\)
On peut choisir \(\alpha _{11}\) comme on veut :soit égal à 1, soit tel que le vecteur soit unitaire \(\left\| {\overrightarrow {{W_1}} } \right\| = 1 = {\alpha _{11}}\sqrt {1 + \frac{{{\ell ^2}}}{4}} \Rightarrow {\alpha _{11}} = \frac{1}{{\sqrt {1 + \frac{{{\ell ^2}}}{4}} }}\)
\(\begin{array}{l} \left( {\frac{4}{{3\ell }}\left[ {\begin{array}{*{20}{c}} g&{ - g\ell /4}\\ { - g/\ell }&g \end{array}} \right] - {\lambda _2}\left[ {\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right]} \right)\left( \begin{array}{l} {\alpha _{12}}\\ {\alpha _{22}} \end{array} \right) = \left( \begin{array}{l} 0\\ 0 \end{array} \right)\\ \left( {\frac{4}{{3\ell }}\left[ {\begin{array}{*{20}{c}} { - g/2}&{ - g\ell /4}\\ { - g/\ell }&{ - g/2} \end{array}} \right]} \right)\left( \begin{array}{l} {\alpha _{12}}\\ {\alpha _{22}} \end{array} \right) = \left( \begin{array}{l} 0\\ 0 \end{array} \right)\\ \left\{ \begin{array}{l} - \frac{g}{2}{\alpha _{12}} - \frac{{g\ell }}{4}{\alpha _{22}} = 0\\ - \frac{g}{\ell }{\alpha _{12}} - \frac{g}{2}{\alpha _{22}} = 0 \end{array} \right. \Rightarrow \left\{ \begin{array}{l} - \frac{g}{2}{\alpha _{12}} - \frac{{g\ell }}{4}{\alpha _{22}} = 0\\ {\alpha _{22}} = - \frac{2}{\ell }{\alpha _{12}} \end{array} \right. \Rightarrow \left\{ \begin{array}{l} - \frac{g}{2}{\alpha _{12}} + \frac{g}{2}{\alpha _{22}} = 0\\ {\alpha _{22}} = - \frac{2}{\ell }{\alpha _{12}} \end{array} \right. \end{array}\)
Donc le 2e vecteur propre est \(\overrightarrow {{W_2}} = {\alpha _{12}}\left( \begin{array}{l} 1\\ - \frac{\ell }{2} \end{array} \right)\)
Finalement, les solutions sont :
\(\begin{array}{l} \bar x = {\alpha _{11}}{A_1}\cos ({\omega _1}t + {\varphi _1}) + {\alpha _{12}}{A_2}\cos ({\omega _2}t + {\varphi _2})\\ \bar \theta = {\alpha _{21}}{A_1}\cos ({\omega _1}t + {\varphi _1}) + {\alpha _{21}}{A_2}\cos ({\omega _2}t + {\varphi _2}) \end{array}\)
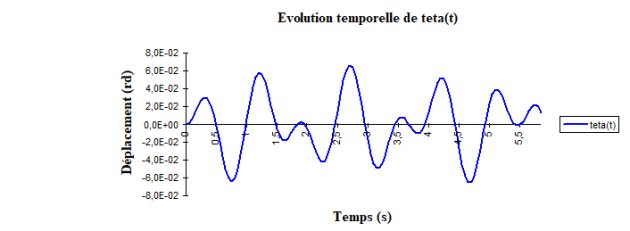
Les courbes ci-dessous présente l’évolution temporelle de \(\bar x(t)\) et \(\bar \theta (t)\) en prenant m=200 g. (M=600 g), l=30 cm, \(k = 4 m.g/l = 26.2 N/m\) et \({x_0} = 1\)cm.
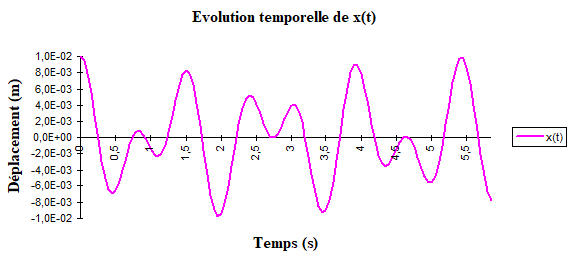
Eléments de correction
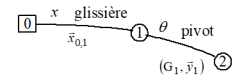
Tableau bilan inconnues/équations complet : (le problème est considéré plan \(({\rm{O}},\overrightarrow {{x_0}} ,\overrightarrow {{z_0}} )\))
| Inconnues | 8 | Equations | 8 |
Cinématique | x, q | 2 |
| 0 |
Dynamique | 1 glissière 1 pivot Ressort amortisseur | 2 2 1 1 | Théorèmes généraux 2 solides * 3 | 6 |
Lois de comportement ressort amortisseur | 1 1 |
Remarque : Le problème est donc isostatique et le degré de liberté est égal à 2.
On définit les torseurs des liaisons comme suit :
Glissière 01 de direction \(\overrightarrow {{x_0}} \left\{ {{T_{0 \to 1}}} \right\} = {\left\{ {\begin{array}{*{20}{c}} 0&{{L_{01}} = 0}\\ {{Y_{01}} = 0}&{{M_{01}}}\\ {{Z_{01}}}&{{N_{01}} = 0} \end{array}} \right\}_{{{\rm{G}}_1},{R_1}}}\)
pivot 12 d’axe \(({{\rm{G}}_{\rm{1}}},\overrightarrow {{y_1}} ) \left\{ {{T_{1 \to 2}}} \right\} = {\left\{ {\begin{array}{*{20}{c}} {{X_{12}}}&{{L_{12}} = 0}\\ {{Y_{12}} = 0}&0\\ {{Z_{12}}}&{{N_{12}} = 0} \end{array}} \right\}_{{{\rm{G}}_1},{R_1}}}\)
L’application des théorèmes généraux à chacun des deux solides et les lois de comportement pour le ressort et l’amortisseur nous permettent d’écrire les 8 équations dynamiques suivantes :
PFD au point \({{\rm{G}}_1}\) pour le pendule : \(\left\{ \begin{array}{l} {\rm{m}}\left( {\ddot x + {\rm{l}}\ddot \theta \cos \theta - {\rm{l}}{{\dot \theta }^2}\sin \theta } \right) = {X_{12}}\\ - {\rm{m}}\left( {{\rm{l}}\ddot \theta \sin \theta + {\rm{l}}{{\dot \theta }^2}\cos \theta } \right) = {Z_{12}} + {\rm{mg}}\\ \\ {\rm{m}}{{\rm{l}}^{\rm{2}}}\ddot \theta + {\rm{ml}}\ddot x\cos \theta = - {\rm{mgl}}\sin \theta \end{array} \right.\)
PFD au point G1 pour le chariot : \(\left\{ \begin{array}{l} {\rm{M}}\ddot x = {F_{{\rm{R1}}}} + {F_{{\rm{A1}}}} + {X_{21}}\\ 0 = {Z_{01}} + {Z_{21}} + {\rm{Mg}}\\ \\ 0 = {M_{01}} \end{array} \right.\)
Pour le ressort : \({F_{{\rm{R1}}}} = - kx\)
Pour l’amortisseur : \({F_{{\rm{A1}}}} = - b\dot x\)