Loi de dérive d’un pneumatique
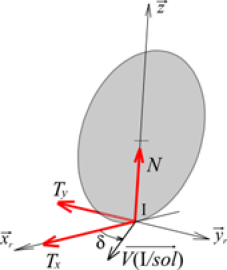
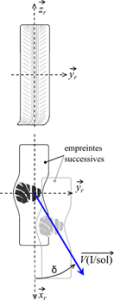
Soit \(\overrightarrow {{x_{roue}}}\) l’axe longitudinal (intersection du plan de jante de la roue et du plan du sol) et \(\overrightarrow {{y_{roue}}}\) l’axe transversal de la roue.
L’angle de dérive est l’angle entre l’axe \(\overrightarrow {{x_{roue}}}\) de la roue la direction de la vitesse du point de contact \({\rm{I}}\) par rapport au sol :
\(\delta = \left( {\overrightarrow {{x_{roue}}} ,\overrightarrow {V\left( {{\rm{I}}/sol} \right)} } \right) = \arctan \left( {\frac{{\overrightarrow {V\left( {{\rm{I}}/sol} \right)} .\overrightarrow {{y_{roue}}} }}{{\overrightarrow {V\left( {{\rm{I}}/sol} \right)} .\overrightarrow {{x_{roue}}} }}} \right)\)
La loi de dérive du pneumatique est \(\overrightarrow {{F_{sol \to roue}}} .\overrightarrow {{y_{roue}}} = - D\delta\)
Où \(D\) est le coefficient de dérive issu d’essais sur le pneumatique.
La résultante des actions de contact est de la forme : \(\overrightarrow {{F_{sol \to roue}}} = {T_x}\overrightarrow {{x_{roue}}} + {T_y}\overrightarrow {{y_{roue}}} + {T_x}\overrightarrow z\)
On considère qu’il y a non glissement \(\overrightarrow {V\left( {{\rm{I,roue}}/sol} \right)} .\overrightarrow {{x_{roue}}} = 0\) et donc \(\sqrt {T_x^2 + T_y^2} < \mu N\).