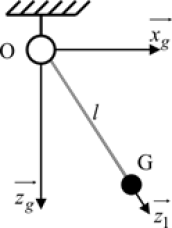
Exemple d’un pendule
Exemple : Illustration avec un pendule simple
Soit un solide considéré comme une masse ponctuelle \(m\) concentrée en \({\rm{G}}\) et en liaison pivot d’axe \(\left( {{\rm{O}}\vec y} \right)\) avec un bâti paramétrée \(\theta = \left( {\overrightarrow {{z_g}} ,\overrightarrow {{z_1}} } \right)\).
\(\begin{array}{l} \overrightarrow {{\rm{OG}}} = l\overrightarrow {{z_1}} \\ \overrightarrow {V{\rm{(G}}/g{\rm{)}}} = \dot \theta \overrightarrow y \wedge l\overrightarrow {{z_1}} = l\dot \theta \overrightarrow {{x_1}} \\ \overrightarrow {\Gamma {\rm{(G}}/g{\rm{)}}} = l\ddot \theta \overrightarrow {{x_1}} + \dot \theta \overrightarrow y \wedge l\dot \theta \overrightarrow {{x_1}} = l\ddot \theta \overrightarrow {{x_1}} - l{{\dot \theta }^2}\overrightarrow {{z_1}} \end{array}\)
Le solide est soumis à la pesanteur \(\overrightarrow {{P_{g \to 1}}} = mg\overrightarrow {{z_g}}.\)
Un couple moteur \(\overrightarrow {{C_{0 \to 1}}({\rm{O}})} = {C_m}\overrightarrow y\) est appliqué entre le bâti et le solide en \({\rm{O}}.\)
Le principe fondamental de la dynamique s’écrit alors :
\(\begin{array}{l} \sum {\overrightarrow {{F_{ext \to S}}} } = m\,\overrightarrow {\Gamma ({\rm{G}}/g)} \Leftrightarrow \left\{ \begin{array}{c} {X_{01}} = m\left( {l\ddot \theta \cos \theta - l{{\dot \theta }^2}\sin \theta } \right)\\ {Y_{01}} + mg = m\left( {l\ddot \theta \sin \theta - l{{\dot \theta }^2}\cos \theta } \right) \end{array} \right.\\ \\ \sum {\overrightarrow {{M_{ext \to S}}{\rm{(O)}}} } = \overrightarrow {{\rm{OG}}} \wedge m\,\overrightarrow {\Gamma ({\rm{G}}/g)} \Leftrightarrow {C_m} = m{l^2}\ddot \theta \end{array}\)
\(m\,{l^2} = {I_{\left( {{\rm{O}}\overrightarrow y } \right)}}\) est appelé « moment d’inertie ».