Position du centre de masse
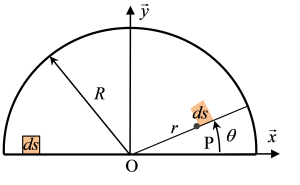
Exemple : Position du centre de masse d’un demi-disque
Demi-disque de masse surfacique \(\rho\) et d’aire \({A_S} = \pi {R^2}/2\)
Le demi-disque a un plan de symétrie \(\left( {{\rm{O}}\overrightarrow {\rm{y}} \overrightarrow {\rm{z}} } \right)\) donc \(\overrightarrow {{\rm{OG}}} .\overrightarrow x = 0\).
\({y_G} = \frac{1}{m}\int_S {y\,dm} = \frac{2}{{\pi {R^2}}}\int_S {y\,\,ds}\)
Soit par changement de variable : \(x = r\cos \theta\) et \(y = r\sin \theta\)
D’où \(ds = rd\theta \,dr\)
Donc \({y_G} = \frac{2}{{\pi {R^2}}}\int_0^\pi {\sin \theta d\theta } \int_0^R {{r^2}dr} = \frac{2}{{\pi {R^2}}}\left[ {\cos \theta } \right]_0^\pi \left[ {\frac{{{r^3}}}{3}} \right]_0^R = \frac{{4R}}{{3\pi }}\)
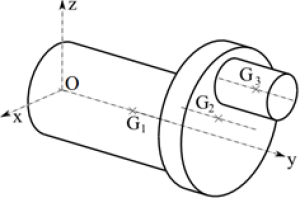
Exemple : Vilebrequin
Soit un vilebrequin formé de trois solides assemblés de masses \({m_1},\) \({m_2}\) et \({m_3}\) et de centres d’inertie respectifs \({{\rm{G}}_1}{\left( {0,{y_{{\rm{G}}1}},0} \right)_R},\) \({{\rm{G}}_2}{\left( {0,{y_{{\rm{G}}2}},{z_{{\rm{G}}2}}} \right)_R}\) et \({{\rm{G}}_3}{\left( {0,{y_{{\rm{G}}3}},{z_{{\rm{G}}3}}} \right)_R}.\)
La position du centre d’inertie de l’ensemble est :
\(\begin{array}{c} \overrightarrow {{\rm{O}}{{\rm{G}}_\Sigma }} = \frac{{{m_1}\overrightarrow {{\rm{O}}{{\rm{G}}_1}} + {m_2}\overrightarrow {{\rm{O}}{{\rm{G}}_2}} + {m_3}\overrightarrow {{\rm{O}}{{\rm{G}}_3}} }}{{{m_1} + {m_2} + {m_3}}}\\ = \frac{1}{{{m_1} + {m_2} + {m_3}}}{\left( \begin{array}{c} 0\\ {m_1}{y_{{\rm{G}}1}} + {m_2}{y_{{\rm{G}}2}} + {m_3} {y_{{\rm{G}}3}}\\ {m_2}{z_{{\rm{G}}2}} + {m_3}{z_{{\rm{G}}3}} \end{array} \right)_R} \end{array}\)
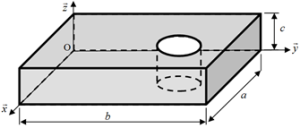
Exemple : Plaque Trouée
Soit une plaque initialement de masse \({m_1}\) et de centre d’inertie \({{\rm{G}}_1}{\left( {\frac{a}{2},\frac{b}{2},\frac{c}{2}} \right)_R}.\) Elle est ensuite percée, le volume du trou aurait une masse \({m_2}\) et son centre d’inertie serait \({{\rm{G}}_2}{\left( {\frac{a}{2},\frac{3}{4}b,\frac{c}{2}} \right)_R}\) s’il était constitué du même matériau que la pièce.
