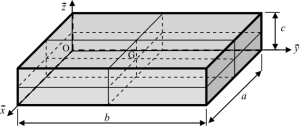
Centre de masse ou d'inertie d'un solide
Le centre de masse \({\rm{G}}\) d’un solide est le barycentre des points \({\rm{P}}\) du solide pondéré par leur masse :
\(\mathop \smallint \limits_S \overrightarrow {{\rm{GP}}} \,dm = \vec 0\quad \Leftrightarrow \quad \int_S {\overrightarrow {{\rm{GO}}} + \overrightarrow {{\rm{OP}}} \,dm} = \overrightarrow 0 \quad \Leftrightarrow \quad {m_S}\overrightarrow {{\rm{OG}}} = \int_S {\overrightarrow {{\rm{OP}}} dm} \quad \Leftrightarrow \quad \overrightarrow {{\rm{OG}}} = \frac{{\int_S {\overrightarrow {{\rm{OP}}} dm} }}{{{m_S}}}\)
Dans un système de coordonnées cartésiennes où la position des points est \(\overrightarrow {{\rm{OP}}} = {\left( {\begin{array}{*{20}{c}} x\\ y\\ z \end{array}} \right)_R}\) alors les coordonnées du centre de masse \(\overrightarrow {{\rm{OG}}} = {\left( {\begin{array}{*{20}{c}} {{x_G}}\\ {{y_G}}\\ {{z_G}} \end{array}} \right)_R}\) sont \(\begin{array}{*{20}{c}} {{x_G} = \frac{1}{{{m_S}}}\int_S {x\,dm} }\\ {{y_G} = \frac{1}{{{m_S}}}\int_S {y\,dm} }\\ {{z_G} = \frac{1}{{{m_S}}}\int_S {z\,dm} } \end{array}\)
Remarque :
Si le solide est homogène et présente un plan de symétrie alors son centre de masse appartient au plan de symétrie.
Par conséquent, le centre de masse d’un solide homogène de révolution se situe sur l’axe de révolution.
La position du centre d’inertie \({{\rm{G}}_\Sigma }\) d’un ensemble de \(i\) solides \({S_i}\), ayant chacun une masse \({m_i}\) et un centre de masse \({{\rm{G}}_i}\), est donnée par : \(\overrightarrow {{\rm{O}}{{\rm{G}}_\Sigma }} = \frac{{\mathop \sum \limits_i \left( {{m_i}\overrightarrow {{\rm{O}}{{\rm{G}}_i}} } \right)}}{{\mathop \sum \limits_i {m_i}}}\)