Equiprojectivité
Si un solide est considéré indéformable alors l’ensemble de ces points gardent entre eux des distances constantes au cours du temps :
Si \({\rm{A}}\) et \({\rm{B}}\) appartiennent à un solide indéformable alors \({\overrightarrow {{\rm{AB}}} ^2} = cste\).
En dérivant par rapport au temps, on obtient \(2\overrightarrow {{\rm{AB}}} {\left( {\frac{{{\rm{d}}\overrightarrow {{\rm{AB}}} }}{{{\rm{dt}}}}} \right)_{{R_i}}} = 0\)
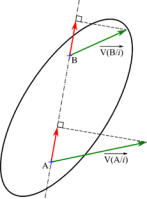
En décomposant le vecteur \(\overrightarrow {{\rm{AB}}}\) en passant par un point \({{\rm{O}}_i}\) fixe dans \({R_i}\) :
\(\overrightarrow {{\rm{AB}}} \left( {{{\left( {\frac{{{\rm{d}}\overrightarrow {{{\rm{O}}_i}{\rm{B}}} }}{{{\rm{dt}}}}} \right)}_{{R_i}}} - {{\left( {\frac{{{\rm{d}}\overrightarrow {{{\rm{O}}_i}{\rm{A}}} }}{{{\rm{dt}}}}} \right)}_{{R_i}}}} \right) = 0\) d’où \(\overrightarrow {{\rm{AB}}} .\overrightarrow {V{\rm{(B}}/i{\rm{)}}} = \overrightarrow {{\rm{AB}}} .\overrightarrow {V{\rm{(A}}/i{\rm{)}}}\)
En divisant par la norme de \(\overrightarrow {{\rm{AB}}},\) il en résulte : \(\frac{{\overrightarrow {{\rm{AB}}} }}{{\left\| {\overrightarrow {{\rm{AB}}} } \right\|}}.\overrightarrow {V{\rm{(B}}/i{\rm{)}}} = \frac{{\overrightarrow {{\rm{AB}}} }}{{\left\| {\overrightarrow {{\rm{AB}}} } \right\|}}.\overrightarrow {V{\rm{(A}}/i{\rm{)}}}\)
Le champ des vitesses d’un solide indéformable est donc équiprojectif.