Champ des vitesses d’un solide
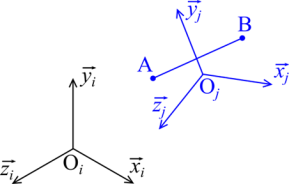
Soit deux points \({\rm{A}}\) et \({\rm{B}}\) fixes dans un repère \({R_j}\) en mouvement par rapport à un repère \({R_i}.\)
On peut exprimer la vitesse du point \({\rm{B}}\) en fonction de celle du point \({\rm{A}}.\)
La vitesse du point \({\rm{B}}\) par rapport au repère \({R_i}\) est par définition :
\(\overrightarrow {V({\rm{B}}/i)} = {\left( {\frac{d}{{dt}}\overrightarrow {{{\rm{O}}_i}{\rm{B}}} } \right)_{{R_i}}}\)
Si on décompose le vecteur position en passant par le point \({\rm{A}},\) on a :
\(\overrightarrow {V({\rm{B}}/i)} = {\left( {\frac{d}{{dt}}\overrightarrow {{{\rm{O}}_i}{\rm{A}}} } \right)_{{R_i}}} + {\left( {\frac{d}{{dt}}\overrightarrow {{\rm{AB}}} } \right)_{{R_i}}}\)
On reconnait alors dans l’expression, la vitesse du point \({\rm{A}}\) par rapport à un repère \({R_i}\) :
\({\left. {\frac{d}{{dt}}\overrightarrow {{{\rm{O}}_i}{\rm{A}}} } \right|_i} = \overrightarrow {V({\rm{A}}/i)}\)
Le vecteur \(\overrightarrow {{\rm{AB}}}\) étant constant dans la base \({R_j},\) sa dérivée par rapport à \({R_i}\) est :
\({\left. {\frac{d}{{dt}}\overrightarrow {{\rm{AB}}} } \right|_i} = {\left. {\frac{d}{{dt}}\overrightarrow {{\rm{AB}}} } \right|_j} + \overrightarrow {{\Omega _{j/i}}} \wedge \overrightarrow {{\rm{AB}}} = \overrightarrow 0 + \overrightarrow {{\Omega _{j/i}}} \wedge \overrightarrow {{\rm{AB}}} = \overrightarrow {{\rm{BA}}} \wedge \overrightarrow {{\Omega _{j/i}}}\)
On obtient alors la relation entre les vitesses de 2 points d’un solide par rapport à un repère. Elle est de la même forme que la relation de champs de moment :
\(\overrightarrow {V({\rm{B}}/i)} = \overrightarrow {V({\rm{A}}/i)} + \overrightarrow {{\Omega _{j/i}}} \wedge \overrightarrow {{\rm{AB}}}\)