Cas d’application : étude cinématique d’un différentiel d’automobile
Un différentiel est un système mécanique qui a pour fonction de distribuer une vitesse de rotation par répartition de l'effort cinématique, de façon adaptative, immédiate et automatique, aux besoins d'un ensemble mécanique.
Par exemple, il est très utile sur un véhicule automobile où il permet aux roues motrices de tourner à des vitesses différentes lors du passage d'une courbe : les roues situées à l'extérieur du virage tournent plus vite que celles situées à l'intérieur.
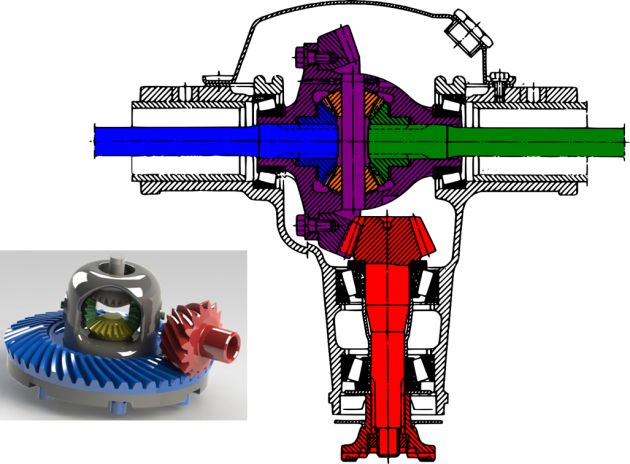

Attention : Graphe des liaisons
Le schéma cinématique ne respecte pas tout à fait la géométrie du dessin d’ensemble ; le principe de fonctionnement est en revanche identique.

Paramétrage et figures de changement de base
Le mouvement du solide i (i = 1, 2, 3, 4) par rapport à 0 est paramétré par l’angle \({{\psi }_{i}}\) ;
Le mouvement du satellite 5 par rapport à la couronne 4 est paramétré par l’angle \(\theta\).
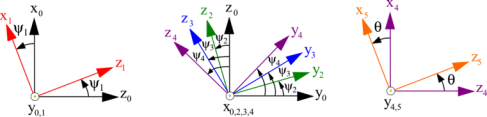
Calcul des vitesses de glissement au point I
Deux méthodes peuvent être employées : par dérivation ou par composition des mouvements et champ des vitesses d’un mouvement.
Le point \(I\) est le point géométrique de contact : il est fixe dans \({{R}_{0}}\).
Méthode : Par dérivation
\(\overrightarrow{V(I,4/1)}=\overrightarrow{V(I/1)}-\overrightarrow{V(I/4)}\)
Avec
\(\begin{align} & \overrightarrow{V(I/4)}={{\left( \frac{d}{dt}\overrightarrow{{{O}_{4}}I} \right)}_{4}}={{\left( \frac{d}{dt}\left( -{{R}_{4}}\overrightarrow{{{Y}_{0}}} \right) \right)}_{4}} \\ & ={{\left( \frac{d}{dt}\left( -{{R}_{4}}\overrightarrow{{{Y}_{0}}} \right) \right)}_{0}}+\overrightarrow{{{\Omega }_{0/4}}}\wedge -{{R}_{4}}\overrightarrow{{{Y}_{0}}} \\ & =\overrightarrow{0}+(-{{{\dot{\psi }}}_{4}}\overrightarrow{{{X}_{0}}})\wedge -{{R}_{4}}\overrightarrow{{{Y}_{0}}}={{R}_{4}}{{{\dot{\psi }}}_{4}}\overrightarrow{{{Z}_{0}}} \end{align}\)
Et
\(\overrightarrow{V(I/1)}={{\left( \frac{d}{dt}\overrightarrow{O_{1}^{*}I} \right)}_{1}}={{\left( \frac{d}{dt}\left( {{R}_{1}}\overrightarrow{{{X}_{0}}} \right) \right)}_{1}}=\overrightarrow{{{\Omega }_{0/1}}}\wedge {{R}_{1}}\overrightarrow{{{X}_{0}}}=(-{{\dot{\psi }}_{1}}\overrightarrow{{{Y}_{0}}})\wedge {{R}_{1}}\overrightarrow{{{X}_{0}}}={{R}_{1}}{{\dot{\psi }}_{1}}\overrightarrow{{{Z}_{0}}}\)
On obtient donc :
\(\overrightarrow{V(I,4/1)}=\left( {{R}_{1}}{{{\dot{\psi }}}_{1}}-{{R}_{4}}{{{\dot{\psi }}}_{4}} \right)\overrightarrow{{{Z}_{0}}}\)
Méthode : Par champ des vitesses
On utilise le point \({{O}_{1}}\), fixe dans le mouvement de 4/1 puisque situé à l’intersection des axes de rotation de 4 et 1 par rapport à 0.
\(\begin{array}{*{35}{l}} \overrightarrow{V(I,4/1)} & =\overrightarrow{V({{O}_{1}},4/1)}+\overrightarrow{{{\Omega }_{4/1}}}\wedge \overrightarrow{{{O}_{1}}I} \\ {} & \begin{align} & =\vec{0}+\left( \overrightarrow{{{\Omega }_{4/0}}}+\overrightarrow{{{\Omega }_{0/1}}} \right)\wedge \overrightarrow{{{O}_{1}}I} \\ & =\left( {{{\dot{\psi }}}_{4}}\overrightarrow{{{X}_{0}}}-{{{\dot{\psi }}}_{1}}\overrightarrow{{{Y}_{0}}} \right)\wedge \left( {{R}_{1}}\overrightarrow{{{X}_{0}}}-{{R}_{4}}\overrightarrow{{{Y}_{0}}} \right) \\ & =\left( {{R}_{1}}{{{\dot{\psi }}}_{1}}-{{R}_{4}}{{{\dot{\psi }}}_{4}} \right)\overrightarrow{{{Z}_{0}}} \\ \end{align} \\ \end{array}\)
Calcul des Vitesses de glissement au point J
J est fixe dans \({{R}_{4}}\).
Méthode : Par dérivation
\(\overrightarrow{V(J,5/3)}=\overrightarrow{V(J/3)}-\overrightarrow{V(J/5)}\)
Avec
\(\begin{align} & \overrightarrow{V(J/3)}={{\left( \frac{d}{dt}\overrightarrow{{{O}_{3}}J} \right)}_{3}}={{\left( \frac{d}{dt}\left( {{R}_{2}}\overrightarrow{{{Y}_{4}}} \right) \right)}_{3}} \\ & =\overrightarrow{{{\Omega }_{4/3}}}\wedge {{R}_{2}}\overrightarrow{{{Y}_{4}}}=\left( {{{\dot{\psi }}}_{4}}-{{{\dot{\psi }}}_{3}} \right)\overrightarrow{{{X}_{0,4}}}\wedge {{R}_{2}}\overrightarrow{{{Y}_{4}}}={{R}_{2}}\left( {{{\dot{\psi }}}_{4}}-{{{\dot{\psi }}}_{3}} \right)\overrightarrow{{{Z}_{4}}} \end{align}\)
Et
\(\begin{align} & \overrightarrow{V(J/5)}={{\left( \frac{d}{dt}\overrightarrow{{{O}_{5}}J} \right)}_{5}}={{\left( \frac{d}{dt}\left( -{{R}_{5}}\overrightarrow{{{X}_{0,4}}} \right) \right)}_{5}} \\ & =\overrightarrow{{{\Omega }_{4/5}}}\wedge -{{R}_{5}}\overrightarrow{{{X}_{0}}}=-\dot{\theta }\overrightarrow{{{Y}_{4,5}}}\wedge -{{R}_{5}}\overrightarrow{{{X}_{0,4}}}=-{{R}_{5}}\dot{\theta }\overrightarrow{{{Z}_{4}}} \end{align}\)
Méthode : Par champ des vitesses
On utilise le point \(O\), fixe dans le mouvement de 5/3 puisque situé à l’intersection des axes de rotation de 5 et 3 par rapport à 4.
\(\begin{array}{*{35}{l}} \overrightarrow{V(J,5/3)} & =\overrightarrow{V(O,5/3)}+\overrightarrow{{{\Omega }_{5/3}}}\wedge \overrightarrow{OJ} \\ {} & \begin{align} & =\vec{0}+\left( \overrightarrow{{{\Omega }_{5/4}}}+\overrightarrow{{{\Omega }_{4/0}}}+\overrightarrow{{{\Omega }_{0/3}}} \right)\wedge \overrightarrow{OJ} \\ & =\left[ \dot{\theta }\overrightarrow{{{Y}_{4,5}}}+\left( {{{\dot{\psi }}}_{4}}-{{{\dot{\psi }}}_{3}} \right)\overrightarrow{{{X}_{4,0}}} \right]\wedge \left( {{R}_{2}}\overrightarrow{{{Y}_{4}}}-{{R}_{5}}\overrightarrow{{{X}_{4,0}}} \right) \\ & =\left[ {{R}_{2}}\left( {{{\dot{\psi }}}_{4}}-{{{\dot{\psi }}}_{3}} \right)+{{R}_{5}}\dot{\theta } \right]\overrightarrow{{{Z}_{4}}} \\\end{align} \\\end{array}\)
Calcul des Vitesses de glissement au point K
De même que pour le point J ! K est fixe dans \({{R}_{4}}\).
Méthode : Par dérivation
\(\overrightarrow{V(K,5/2)}=\overrightarrow{V(K/2)}-\overrightarrow{V(K/5)}\)
Avec \(\overrightarrow{V(K/2)}=\overrightarrow{V(K,4/2)}={{R}_{2}}\left( {{{\dot{\psi }}}_{4}}-{{{\dot{\psi }}}_{2}} \right)\overrightarrow{{{Z}_{4}}}$ et $\overrightarrow{V(K/5)}=\overrightarrow{V(K,4/5)}={{R}_{5}}\dot{\theta }\overrightarrow{{{Z}_{4}}}\)
Donc
\(\overrightarrow{V(K,5/2)}=\left[ {{R}_{2}}\left( {{{\dot{\psi }}}_{4}}-{{{\dot{\psi }}}_{2}} \right)-{{R}_{5}}\dot{\theta } \right]\overrightarrow{{{Z}_{4}}}\)
Méthode : Par champ des vitesses
\(\begin{align} & \overrightarrow{V(K,5/2)}=\overrightarrow{V(O,5/2)}+\overrightarrow{{{\Omega }_{5/2}}}\wedge \overrightarrow{OK} \\ & =\left[ {{R}_{2}}\left( {{{\dot{\psi }}}_{4}}-{{{\dot{\psi }}}_{2}} \right)-{{R}_{5}}\dot{\theta } \right]\overrightarrow{{{Z}_{4}}} \end{align}\)
Cas particuliers de fonctionnement
En ligne droite sur sol sec : \({{\dot{\psi }}_{4}}={{\dot{\psi }}_{2}}={{\dot{\psi }}_{3}}\quad ;\quad \dot{\theta }=0\)
En virage : \({{\dot{\psi }}_{2}}>{{\dot{\psi }}_{3}}\ \text{ou}\ {{\dot{\psi }}_{2}}<{{\dot{\psi }}_{3}}\quad ;\quad {{\dot{\psi }}_{4}}=\frac{{{{\dot{\psi }}}_{2}}+{{{\dot{\psi }}}_{3}}}{2}\quad ;\quad \dot{\theta }\ne 0\)
Une roue bloquée : \({{\dot{\psi }}_{3}}=0\Rightarrow {{\dot{\psi }}_{2}}=2{{\dot{\psi }}_{4}}\quad ;\quad \dot{\theta }\ne 0\)

Différentiel bloqué : \({{\dot{\psi }}_{4}}={{\dot{\psi }}_{2}}={{\dot{\psi }}_{3}}\quad ;\quad \dot{\theta }=0\)
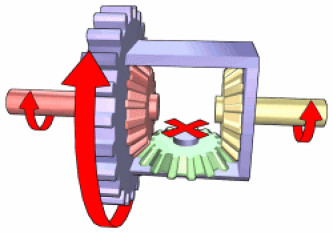
Sur banc, moteur arrêté, 1 vitesse enclenchée : \({{\dot{\psi }}_{4}}=0\quad\) ; \(\quad {{\dot{\psi }}_{3}}=-{{\dot{\psi }}_{2}}\quad\) ; \(\quad \dot{\theta }=\frac{{{R}_{2}}}{{{R}_{5}}}{{\dot{\psi }}_{3}}\)
