Vitesse instantanée de rotation
La vitesse de rotation instantanée d’un solide autour d’un axe (pas nécessairement fixe) par rapport à un référentiel \({R_i}\) est définie comme la limite de la variation de sa position angulaire \(\Delta \theta\) orientée suivant l’axe de rotation, entre deux instants séparés d’une durée \(\Delta t,\) divisée par cette durée \(\Delta t\) quand la durée \(\Delta t\) tend vers zéro :
\(\overrightarrow {{\Omega _{j/i}}} = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta \theta }}{{\Delta t}}\overrightarrow {\rm{u}} = \frac{{d\theta }}{{dt}}\overrightarrow {\rm{u}} = \dot \theta \overrightarrow {\rm{u}}\)
Exemple : Rotation d’un repère
Rotation de \({R_1}\) par rapport à \({R_0}\) autour d’un axe commun \(\overrightarrow {{z_{0,1}}}.\)
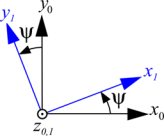
La rotation est paramétrée par \(\psi = \left( {\overrightarrow {{x_0}} ,\overrightarrow {{x_1}} } \right) = \left( {\overrightarrow {{y_0}} ,\overrightarrow {{y_1}} } \right)\)
La vitesse de rotation est : \(\overrightarrow {{\Omega _{1/0}}} = \dot \psi \overrightarrow {{z_{0,1}}}\)
Ce vecteur « vitesse de rotation » exprimé dans une autre base peut avoir plusieurs composantes.
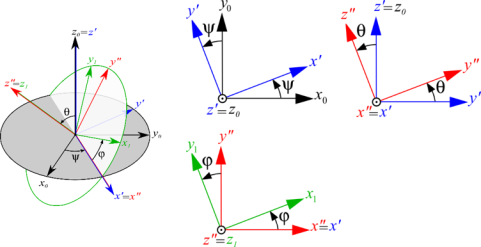
Si on paramètre l’orientation d’un \({R_1}\left( {{{\rm{O}}_{\rm{1}}},\overrightarrow {{x_1}} ,\overrightarrow {{y_1}} ,\overrightarrow {{z_1}} } \right)\) par rapport à un repère \({R_0}\left( {{{\rm{O}}_{\rm{0}}},\overrightarrow {{x_0}} ,\overrightarrow {{y_0}} ,\overrightarrow {{z_0}} } \right)\) avec les angles d’Euler (de type 1), c'est-à-dire par 3 rotations successives alors la vitesse de rotation du solide est la somme des trois vitesses de rotations relatives :
\(\Omega_{1/0}=\Omega_{1/R^{''}} + \Omega_{ R^{''} / R^{'}} + \Omega_{R^{'}/0}=\dot{\phi}_{z_{R^{''},1}} + \dot{\theta}_{x_{R^{''},R^{'}}}+\dot{\psi}_{z_{R^{'},0}}\)
En l’exprimant dans la base \(R'\) par exemple, on a : \(\overrightarrow {{\Omega _{1/0}}} = \dot \phi \cos \theta \overrightarrow {{z_{R'}}} - \dot \phi \sin \theta \overrightarrow {{y_{R'}}} + \dot \theta \overrightarrow {{x_{R'}}} + \dot \psi \overrightarrow {{z_{R'}}}\)
Soit \(\overrightarrow {{\Omega _{1/0}}} = {\left( \begin{array}{l} {\dot \theta }\\ - \dot \phi \sin \theta \\ \dot \psi + \dot \phi \cos \theta \end{array} \right)_{R'}}\)
Remarque :
On peut trouver une base où ce vecteur n’aura qu’une seule composante.
Un point \({{\rm{P}}_j}\) d’un solide \(j\) en rotation autour d’un axe \({{\rm{O}}_i}\overrightarrow {{z_{i,j}}}\) paramétrée par l’angle \(\theta\) par rapport à un repère \({R_i}\) a une vitesse \(\overrightarrow {V({\rm{P}}/i)} = {\left. {\frac{d}{{dt}}\overrightarrow {{{\rm{O}}_i}{{\rm{P}}_j}} } \right|_i}\)
Si \(\overrightarrow {{{\rm{O}}_i}{{\rm{P}}_{\rm{j}}}} = r\overrightarrow {{x_j}}\) avec \(r = cst\) alors \(\overrightarrow {V({{\rm{P}}_j}/i)} = r\dot \theta \overrightarrow {{y_j}}.\)

Dans le cas général, cette relation se traduit par \(\overrightarrow {V({{\rm{P}}_{\rm{j}}}/i)} = \overrightarrow {{\Omega _{j/i}}} \wedge \overrightarrow {{{\rm{O}}_i}{{\rm{P}}_j}}\)