Joint de Cardan
Le joint de Cardan permet la transmission d'une rotation angulaire entre deux arbres dont les axes géométriques concourent en un même point.
Cette technique est utilisée sur les véhicules pour accoupler deux arbres tournants non alignés ou dont les positions angulaires de l'un par rapport à l'autre peuvent varier ; par exemple l'axe du volant et le boîtier de direction, surtout dans le cas d'un volant réglable en hauteur par rapport au conducteur.

L'invention de ce joint en 1545 est attribuée au mathématicien italien Girolamo Cardano (Jérôme Cardan en français). Ce célèbre savant italien se serait inspiré d'un compas de marine fixé sur deux cercles articulés. Il a décrit l'articulation portant son nom dans un traité de physique intitulé « De subtilitate rerum ».

Le joint de Cardan est constitué :
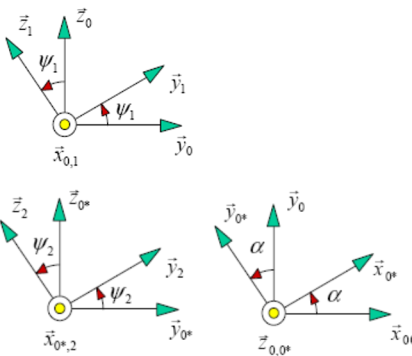
d’un arbre d’entrée (1) en liaison pivot avec le bâti (0) paramétrée \({\psi _1} = (\overrightarrow {{y_0}} ,\overrightarrow {{y_1}} ) = (\overrightarrow {{z_0}} ,\overrightarrow {{z_1}} )\)
d’un arbre de sortie (2) en liaison pivot avec le bâti (0) paramétré \({\psi _2} = (\overrightarrow {{y_0*}} ,\overrightarrow {{y_2}} ) = (\overrightarrow {{z_0*}} ,\overrightarrow {{z_2}} )\)
d’un croisillon (3) en liaison pivot avec l’arbre d’entrée (1) et avec arbre de sortie (2) ; les axes de ces 2 liaisons pivot sont perpendiculaires. Ces liaisons pivot ne sont pas paramétrées.
L’arbre de sortie (2) est désaxé de l’arbre d’entrée (1) d’un angle \(\alpha = (\overrightarrow {{x_0}} ,\overrightarrow {{x_{0*}}} ) = cste\).


Question
Écrire la (ou les) équation(s) de joint imposée(s) par le croisillon (3).
Solution
Le croisillon impose que les axes des pivots 1/3 et 2/3 soient perpendiculaires.
\(\overrightarrow {{y_2}} \bot \overrightarrow {{z_1}} \quad \Rightarrow \quad \overrightarrow {{y_2}} .\overrightarrow {{z_1}} = 0\)
\(\overrightarrow {{y_2}} .\overrightarrow {{z_1}} = \left( {\cos {\psi _2}\overrightarrow {{y_{0*}}} + \sin {\psi _2}\overrightarrow {{z_{0*}}} } \right).\left( {\cos {\psi _1}\overrightarrow {{z_0}} - \sin {\psi _1}\overrightarrow {{y_0}} } \right) = 0\)
\(\overrightarrow {{y_2}} .\overrightarrow {{z_1}} = \left( {\cos {\psi _2}\left( {\cos \alpha \overrightarrow {{y_0}} - \sin \alpha \overrightarrow {{x_0}} } \right) + \sin {\psi _2}\overrightarrow {{z_0}} } \right).\left( {\cos {\psi _1}\overrightarrow {{z_0}} - \sin {\psi _1}\overrightarrow {{y_0}} } \right) = 0\)
\(\overrightarrow {{y_2}} .\overrightarrow {{z_1}} = \sin {\psi _2}\cos {\psi _1} - \cos \alpha \cos {\psi _2}\sin {\psi _1} = 0\)
\(\overrightarrow {{y_2}} .\overrightarrow {{z_1}} = \tan {\psi _2} - \cos \alpha \tan {\psi _1} = 0\)
\(\tan {\psi _2} = \cos \alpha \tan {\psi _1}\)
Question
En déduire le degré de mobilité du mécanisme.
Solution
2 paramètres cinématiques \({\psi _1},\) \({\psi _2}.\)
1 équation de liaison de type géométrique \(\tan {\psi _2} = \cos \alpha \tan {\psi _1}\)
Donc 1 paramètre cinématique indépendant ou mobilité.
Question
Calculer le rapport des vitesses \(\frac{{{{\dot \psi }_2}}}{{{{\dot \psi }_1}}},\) le joint de Cardan est-il homocinétique ?
Solution
On dérive l’équation de liaison par rapport au temps :
\({\dot \psi _2}\left( {1 + {{\tan }^2}{\psi _2}} \right) = \cos \alpha \;{\dot \psi _1}\left( {1 + {{\tan }^2}{\psi _1}} \right)\)
Rappel :
\(\frac{d}{{dx}}\tan x = 1 + {\tan ^2}x = \frac{1}{{{{\cos }^2}x}}\)
On obtient donc le rapport de vitesses suivant :
\(\rho = \frac{{{{\dot \psi }_2}}}{{{{\dot \psi }_1}}} = \cos \alpha \frac{{1 + {{\tan }^2}{\psi _1}}}{{1 + {{\tan }^2}{\psi _2}}}\)
On remplace
\(\tan {\psi _2}\) grâce à l’équation de liaison pour obtenir un rapport de vitesse uniquement fonction de \({\psi _1}\).
\(\rho = \frac{{{{\dot \psi }_2}}}{{{{\dot \psi }_1}}} = \cos \alpha \frac{{1 + {{\tan }^2}{\psi _1}}}{{1 + {{\tan }^2}{\psi _1}{{\cos }^2}\alpha }}\)
Le rapport des vitesses n’est pas constant et évolue en fonction l’angle \({\psi _1}\), le joint de cardan n’est donc pas homocinétique.

\(\begin{array}{l} {\psi _1} = 0\quad \Rightarrow \quad \tan {\psi _1} = 0\quad \Rightarrow \quad \frac{{{{\dot \psi }_2}}}{{{{\dot \psi }_1}}} = \cos \alpha \\ {\psi _1} = \frac{\pi }{4}\quad \Rightarrow \quad \tan {\psi _1} = 1\quad \Rightarrow \quad \frac{{{{\dot \psi }_2}}}{{{{\dot \psi }_1}}} = \frac{{2\cos \alpha }}{{1 + {{\cos }^2}\alpha }} \approx 1\quad si\;\alpha \;petit\\ {\psi _1} = \frac{\pi }{2}\quad \Rightarrow \quad \tan {\psi _1} \to \infty \quad \Rightarrow \quad \frac{{{{\dot \psi }_2}}}{{{{\dot \psi }_1}}} \to \frac{1}{{\cos \alpha }} \end{array}\)