Exemple de changement de base du cas des angles d’Euler (de type 1)
Soit un vecteur \(\overrightarrow V = {v_{xj}}\overrightarrow {{x_j}} + {v_{yj}}\overrightarrow {{y_j}} + {v_{zj}}\overrightarrow {{z_j}}\)
\({\left( \begin{array}{l}{v_{xi}}\\{v_{yi}}\\{v_{zi}}\end{array} \right)_{{R_i}}} = \left[ {\begin{array}{*{20}{r}}{\cos \psi }&{ - \sin \psi }&0\\{\sin \psi }&{\cos \psi }&0\\0&0&1\end{array}} \right]{\left( \begin{array}{l}{v_{x'}}\\{v_{y'}}\\{v_{z'}}\end{array} \right)_{R'}}\)
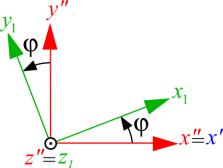
\({\left( \begin{array}{l}{v_{xi}}\\{v_{yi}}\\{v_{zi}}\end{array} \right)_{{R_i}}} = \left[ {\begin{array}{*{20}{c}}{\cos \psi }&{ - \sin \psi }&0\\{\sin \psi }&{\cos \psi }&0\\0&0&1\end{array}} \right]\left[ {\begin{array}{*{20}{c}}1&0&0\\0&{\cos \theta }&{ - \sin \theta }\\0&{\sin \theta }&{\cos \theta }\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{\cos \phi }&{ - \sin \phi }&0\\{\sin \phi }&{\cos \phi }&0\\0&0&1\end{array}} \right]{\left( \begin{array}{l}{v_{xj}}\\{v_{yj}}\\{v_{zj}}\end{array} \right)_{{R_j}}}\)
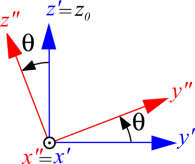
\({\left( \begin{array}{l}{v_{xi}}\\{v_{yi}}\\{v_{zi}}\end{array} \right)_{{R_i}}} = \left[ {\begin{array}{*{20}{c}}{\cos \psi }&{ - \sin \psi \cos \theta }&{\sin \psi \sin \theta }\\{\sin \psi }&{\cos \psi \cos \theta }&{ - \cos \psi \sin \theta }\\0&{\sin \theta }&{\cos \theta }\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{\cos \phi }&{ - \sin \phi }&0\\{\sin \phi }&{\cos \phi }&0\\0&0&1\end{array}} \right]{\left( \begin{array}{l}{v_{xj}}\\{v_{yj}}\\{v_{zj}}\end{array} \right)_{{R_j}}}\)
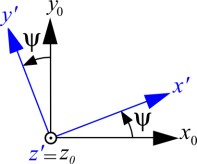
\({\left( \begin{array}{l}{v_{xi}}\\{v_{yi}}\\{v_{zi}}\end{array} \right)_{{R_i}}} = \left[ {\begin{array}{*{20}{c}}{\cos \psi \cos \phi - \sin \psi \cos \theta \sin \phi }&{ - \cos \psi \sin \phi - \sin \psi \cos \theta \cos \phi }&{\sin \psi \sin \theta }\\{\sin \psi \cos \phi + \cos \psi \cos \theta \sin \phi }&{ - \sin \psi \sin \phi + \cos \psi \cos \theta \cos \phi }&{ - \cos \psi \sin \theta }\\{\sin \theta \sin \phi }&{\sin \theta \cos \phi }&{\cos \theta }\end{array}} \right]{\left( \begin{array}{l}{v_{xj}}\\{v_{yj}}\\{v_{zj}}\end{array} \right)_{{R_j}}}\)