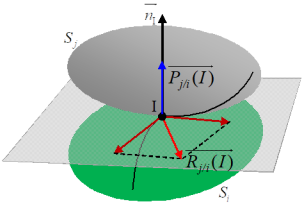
Roulement et pivotement
Le vecteur de vitesse de rotation instantanée entre deux solides \(i\) et \(j\) en contact au point \({\rm{I}}\) peut être décomposé en deux parties : \(\overrightarrow {{\Omega _{j/i}}} = \overrightarrow {{P_{j/i}}({\rm{I}})} + \overrightarrow {{R_{j/i}}({\rm{I}})}\)
le pivotement est la composante suivant \(\overrightarrow {{n_{\rm{I}}}}\) la normale à la surface de contact : \(\overrightarrow {{P_{j/i}}({\rm{I}})} = \left( {\overrightarrow {{\Omega _{j/i}}} .\overrightarrow {{n_{\rm{I}}}} } \right)\overrightarrow {{n_{\rm{I}}}}\)
le roulement est la composante dans le plan tangent : \(\overrightarrow {{R_{j/i}}({\rm{I}})} = \overrightarrow {{\Omega _{j/i}}} - \overrightarrow {{P_{j/i}}({\rm{I}})}\) ou \(\overrightarrow {{R_{j/i}}({\rm{I}})} = \overrightarrow {{n_{\rm{I}}}} \wedge \left( {\overrightarrow {{\Omega _{j/i}}} \wedge \overrightarrow {{n_{\rm{I}}}} } \right)\)