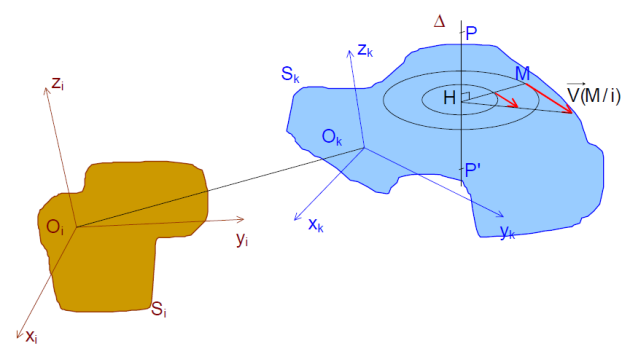
Cinématique des systèmes mécaniques

Dans un mouvement de rotation d’un solide \(k\) par rapport à un solide \(i\), l’ensemble des points \({\rm{P}}\) situés sur l’axe de rotation ont une vitesse nulle \(\overrightarrow {V({\rm{P,}}k/i)}  = \overrightarrow 0\) et les autres points \({\rm{M}}\) du solide ont une vitesse proportionnelle à leur distance à l’axe \(\overrightarrow {V({\rm{M,k}}/i)}  = \overrightarrow {V({\rm{P,k}}/i)}  + \overrightarrow {{\rm{MP}}}  \wedge \overrightarrow {{\Omega _{k/i}}}  = \overrightarrow {V({\rm{P,}}k/i)}  + \overrightarrow {{\rm{HP}}}  \wedge \overrightarrow {{\Omega _{k/i}}}\) (\({\rm{H}}\) projection du point \({\rm{M}}\) sur l’axe de rotation).

Le torseur cinématique a donc la forme suivante sur l’axe de rotation : \({\left\{ {{V_{k/i}}} \right\}_{\rm{P}}} = \left\{ {\left. {\overrightarrow {{\Omega _{k/i}}} } \right|\overrightarrow 0 } \right\}\)

Un solide est animé d’un mouvement de rotation par rapport à un autre si deux points (formant un axe) liés au premier restent fixes par rapport au second au cours du mouvement.