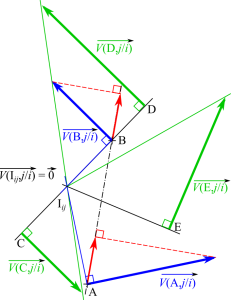
Positionnement du centre instantané de rotation (CIR)
\(\overrightarrow {{\rm{AI}}} = \frac{{\overrightarrow {{\Omega _{j/i}}} \wedge \overrightarrow {V({\rm{A,}}j/i)} }}{{{{\overrightarrow {{\Omega _{j/i}}} }^2}}} + k\overrightarrow {{\Omega _{j/i}}}\)
Dans le cas d'un mouvement plan, les points A et I appartiennent au plan : ce qui signifie que \(\overrightarrow {{\rm{AI}}} .\vec n = 0 \Rightarrow k = 0.\)
On en déduit que le vecteur \(\overrightarrow {{\rm{AI}}}\) est perpendiculaire à \(\overrightarrow {{\Omega _{j/i}}}\) (évident car \(\overrightarrow {{\Omega _{j/i}}}\) est perpendiculaire au plan) et à \(\overrightarrow {V({\rm{A,}}j/i)}\). Ce qui signifie que le centre instantané de rotation se situe sur la droite perpendiculaire à \(\overrightarrow {V({\rm{A,}}j/i)}\) passant par le point A.
Si on connait les vitesses (non colinéaires) de deux points dans le mouvement alors on peut positionner graphiquement le centre instantané de rotation à l'intersection des deux droites passant par le point et perpendiculaire à la vitesse du point.
Cas particulier de la translation : le centre instantané de rotation est rejeté à l'infini perpendiculairement aux vitesses des points.
Cas particulier de la rotation : le centre de la rotation est le CIR.
Méthode :
Positionner le centre instantané de rotation (CIR) d’un mouvement plan
A partir des vitesses de 2 points dans ce mouvement
\(\left. \begin{array}{l} \overrightarrow {{\rm{A}} {{\rm{I}}_{ij}}} \bot \overrightarrow {V({\rm{A,}}\,j/i)} \\ \overrightarrow {{\rm{B}}{{\rm{I}}_{ij}}} \bot \overrightarrow {V({\rm{B,}}\,j/i)} \end{array} \right\} \Rightarrow {{\rm{I}}_{ij}}\)
Le CIR \({{\rm{I}}_{ij}}\) d’un mouvement plan est à l’intersection des perpendiculaires aux vitesses des points dans ce mouvement.
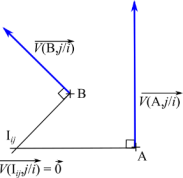
Déterminer graphiquement ou analytiquement la vitesse d’un point dans un mouvement plan
A partir de la vitesse d’un point dans le mouvement et de la position du CIR
\(\overrightarrow {V({\rm{B,}}\,j/i)} = \overrightarrow {V({\rm{A,}}\,j/i)} + \overrightarrow {{\rm{BA}}} \wedge \overrightarrow {{\Omega _{j/i}}}\)
A partir de vitesses du point dans d’autres mouvements
\(\overrightarrow {V({\rm{B,}}\,j/i)} = \overrightarrow {V({\rm{B,}}\,j/k)} + \overrightarrow {V({\rm{B,}}\,k/i)}\)
La vitesse du CIR d’un mouvement plan est nulle dans ce mouvement \(\overrightarrow {V({{\rm{I}}_{ij}}{\rm{,}}\,j/i)} = \overrightarrow 0\)
Lorsqu’il y a non-glissement au point de contact entre 2 solides, cela signifie que la vitesse du point géométrique de contact est nulle dans le mouvement des 2 solides en contact. Le point de contact où il y a non glissement est donc le CIR du mouvement relatif des 2 solides en contact.
Lorsque le mouvement d’un système est contenu dans un plan, on peut utiliser une méthode graphique pour déterminer les vitesses grâce aux propriétés d’équiprojectivité et de champ des vitesses.
\(\overrightarrow {V({\rm{A}},j/i)} .\frac{{\overrightarrow {AB} }}{{\left\| {\overrightarrow {AB} } \right\|}} = \overrightarrow {V({\rm{B}},j/i)} .\frac{{\overrightarrow {AB} }}{{\left\| {\overrightarrow {AB} } \right\|}}\)