Calculer torseur équivalent (ex. barrage droit)
Soit un barrage d’envergure \(L\) dont la surface en contact avec le fluide à un profil linéaire vertical.
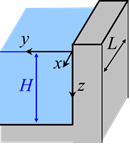
Les points \({\rm{M}}\left( {y,z(y)} \right)\) de la surface du barrage sont définis dans le plan \(\left( {y,z} \right)\) par la relation : \(z(y) = 0\).
La pression du fluide \(p(z) = \rho gz\) exerce sur une surface élémentaire \(dS = L.dl\) un effort élémentaire \(\overrightarrow {dF} = p(z)dS\overrightarrow {{n_{\rm{M}}}}\) avec \(\overrightarrow {{n_{\rm{M}}}}\) la normale à la surface au point \({\rm{M}},\) \(z\) la distance du point \({\rm{M}}\) à la surface de l’eau et \(\rho\) la masse volumique du fluide.
Donc \(\overrightarrow {dF} = - \rho gzLdz\overrightarrow y\)
Question
Déterminer l’action résultant de la pression exercée par le fluide sur le barrage.
Solution
Calcul de la résultante
\(\overrightarrow {{R_{e \to b}}} = \int {\overrightarrow {dF} } = - \int_0^H {\rho gzL\,dz} \overrightarrow y = - \rho gL\left[ {\frac{{{z^2}}}{2}} \right]_0^H\overrightarrow y = - \rho gL\frac{{{H^2}}}{2}\overrightarrow y\)
Calcul du moment résultant en A
\(\overrightarrow {{M_{e \to b}}({\rm{A}})} = \int {\overrightarrow {dM({\rm{A}})} } = \int {\overrightarrow {{\rm{AM}}} \wedge \overrightarrow {dF} } = \int {\left( {\begin{array}{*{20}{c}} 0\\ 0\\ z \end{array}} \right) \wedge \left( {\begin{array}{*{20}{c}} 0\\ { - \rho gzLdz}\\ 0 \end{array}} \right)} = \rho gL\int_0^H {{z^2}dz} \overrightarrow x = \rho gL\frac{{{H^3}}}{3}\overrightarrow x\)
Question
Déterminer les coordonnées du centre de poussée.
Solution
Calcul de l’Automoment : \(\overrightarrow {{R_{e \to b}}} .\overrightarrow {{M_{e \to b}}({\rm{A}})} = - \rho gL\frac{{{H^2}}}{2}\overrightarrow y .\rho gL\frac{{{H^3}}}{3}\overrightarrow x = 0\)
\(\overrightarrow {{R_{e \to b}}} \ne \overrightarrow 0 \quad \Rightarrow \quad\) il existe un point \({\rm{P}}\) où le moment est nul \(\overrightarrow {{M_{e \to b}}({\rm{P}})} = \overrightarrow 0\), c'est-à-dire où l’action peut être représenter par un glisseur.
Le centre de poussée est un point de l’axe central où le moment est minimum et donc égal à 0 dans le cas présent. On va donc déterminer l’axe central du torseur.
\(\overrightarrow {{\rm{A}}{{\rm{P}}^{\rm{*}}}} = \frac{{\overrightarrow {{R_{e \to b}}} \wedge \overrightarrow {{M_{e \to b}}({\rm{A}})} }}{{{{\overrightarrow {{R_{e \to b}}} }^2}}} = \frac{{ - \rho gL\frac{{{H^2}}}{2}\overrightarrow y \wedge \rho gL\frac{{{H^3}}}{3}\overrightarrow x }}{{{{\left( { - \rho gL\frac{{{H^2}}}{2}} \right)}^2}}} = \frac{{\frac{{{H^5}}}{6}\overrightarrow z }}{{\frac{{{H^4}}}{4}}} = \frac{{2}}{3}H\overrightarrow z\)
\(\overrightarrow {{\rm{AP}}} = \frac{{\overrightarrow {{R_{e \to b}}} \wedge \overrightarrow {{M_{e \to b}}({\rm{A}})} }}{{{{\overrightarrow {{R_{e \to b}}} }^2}}} + \lambda \overrightarrow {{R_{e \to b}}} = \frac{{^2}}{3}H\overrightarrow z + k\overrightarrow y\)
On aurait pu aussi déterminer les coordonnées de l’ensemble des points \({\rm{P}}\) dont le moment est nul.
\(\overrightarrow {{M_{e \to b}}({\rm{P}})} = \overrightarrow {{M_{e \to b}}({\rm{A}})} + \overrightarrow {{\rm{PA}}} \wedge \overrightarrow {{R_{e \to b}}} \int {\overrightarrow {dM({\rm{A}})} } = \rho gL\frac{{{H^3}}}{3}\overrightarrow x + \left( {\begin{array}{*{20}{c}} 0\\ {0 - {y_{\rm{P}}}}\\ {0 - {z_{\rm{P}}}} \end{array}} \right) \wedge \left( {\begin{array}{*{20}{c}} 0\\ { - \rho gL\frac{{{H^2}}}{2}}\\ 0 \end{array}} \right) = \rho gL\left( {\frac{{{H^3}}}{3} - \frac{{{H^2}}}{2}{z_{\rm{P}}}} \right)\overrightarrow x\)
\(\overrightarrow {{M_{e \to b}}({\rm{P}})} = \overrightarrow 0 \quad \Leftrightarrow \quad \frac{{{H^3}}}{3} - \frac{{{H^2}}}{2}{z_{\rm{P}}} = 0\quad \Rightarrow \quad {z_{\rm{P}}} = \frac{2}{3}H\) : C’est l’équation d’une droite horizontale.