Torseurs équivalents
Deux torseurs sont équivalents si leurs éléments de réduction exprimés au même point sont égaux :
\(\left\{ {{T_{\rm{1}}}} \right\} = \left\{ {{T_{\rm{2}}}} \right\}\quad \Leftrightarrow \quad \left\{ {\begin{array}{*{20}{l}} {\overrightarrow {{R_1}} = \overrightarrow {{R_2}} }\\ {\overrightarrow {{M_1}({\rm{A}})} = \overrightarrow {{M_2}({\rm{A}})} } \end{array}} \right.\)
Torseur équivalent à la somme de 2 torseurs
\(\left\{ {{T_{{\rm{1}} + {\rm{2}}}}} \right\} = \left\{ {{T_{\rm{1}}}} \right\} + \left\{ {{T_{\rm{2}}}} \right\} = \left\{ {\begin{array}{*{20}{l}} {\overrightarrow {{R_{1 + 2}}} = \overrightarrow {{R_1}} + \overrightarrow {{R_2}} }\\ {\overrightarrow {{M_{1 + 2}} ({\rm{A}})} = \overrightarrow {{M_1}({\rm{A}})} + \overrightarrow {{M_2}({\rm{A}})} = \overrightarrow {{M_1}({{\rm{P}}_1})} + \overrightarrow {{\rm{A}}{{\rm{P}}_1}} \wedge \overrightarrow {{R_1}} + \overrightarrow {{M_2}({{\rm{P}}_2})} + \overrightarrow {{\rm{A}}{{\rm{P}}_2}} \wedge \overrightarrow {{R_2}} } \end{array}} \right.\)
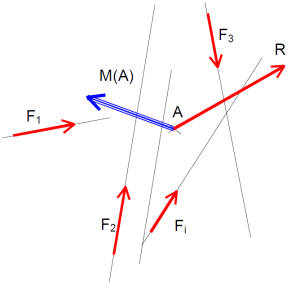
Torseur équivalent à un ensemble fini de glisseurs
Le torseur équivalent à un ensemble fini de glisseur est défini par :
\(\left\{ {{T_{{\rm{eq}}}}} \right\} = \sum\limits_i {\left\{ {{T_{\rm{i}}}} \right\}} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {\overrightarrow {{R_{eq}}} = \sum\limits_i {\overrightarrow {{F_i}} } }\\ {\overrightarrow {{M_{eq}}({\rm{A}})} = \sum\limits_i {\overrightarrow {{M_i}({\rm{A}})} = \sum\limits_i {\overrightarrow {{\rm{A}}{{\rm{P}}_i}} \wedge \overrightarrow {{F_i}} } } } \end{array}} \right.\)
\({{\rm{P}}_i}\) un point du support du vecteur \(\overrightarrow i.\)
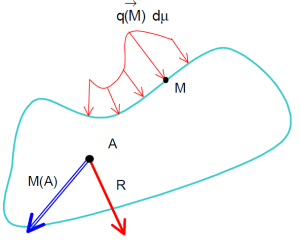
Torseur équivalent à un ensemble infini de glisseurs
Le torseur équivalent à un ensemble infini de glisseur \(\overrightarrow {q({\rm{M}})} \,d\mu\) associé à un domaine \(D\) de l’espace (courbe, surface, volume) est défini par :
\(\left\{ {{T_{{\rm{eq}}}}} \right\} = \left\{ {\begin{array}{*{20}{l}} {\overrightarrow {{R_{eq}}} = \int_D {\overrightarrow {q({\rm{M}})} \,d\mu } }\\ {\overrightarrow {{M_{eq}}({\rm{A}})} = \int_D {\overrightarrow {{\rm{AM}}} \wedge \overrightarrow {q({\rm{M}})} \,d\mu } } \end{array}} \right.\)
Torseur équivalent à un ensemble de glisseurs concourants
Le torseur équivalent à un ensemble de glisseurs concourants est un glisseur dont le support passe par le point de concours et orienté suivant la résultante :
\(\left\{ {{T_{{\rm{eq}}}}} \right\} = \sum\limits_i {\left\{ {{T_{\rm{i}}}} \right\}} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {\overrightarrow {{R_{eq}}} = \sum\limits_i {\overrightarrow {{V_i}} } }\\ {\overrightarrow {{M_{eq}}({\rm{O}})} = \sum\limits_i {\overrightarrow {{\rm{O}}{{\rm{A}}_i}} \wedge \overrightarrow {{V_i}} = \overrightarrow 0 } } \end{array}} \right.\)

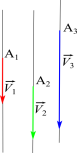
Torseur équivalent à un ensemble de glisseurs parallèles
Le torseur équivalent à un ensemble de glisseurs parallèles est un glisseur dont le support passe par le barycentre des points pondérés par la norme des vecteurs glissants :
\(\left\{ {{T_{{\rm{eq}}}}} \right\} = \sum\limits_i {\left\{ {{T_{\rm{i}}}} \right\}} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {\overrightarrow {{R_{eq}}} = \sum\limits_i {\overrightarrow {{V_i}} } }\\ {\overrightarrow {{M_{eq}}({\rm{G}})} = \sum\limits_i {\overrightarrow {{\rm{G}}{{\rm{A}}_i}} \wedge \overrightarrow {{V_i}} = \sum\limits_i {\overrightarrow {{\rm{G}}{{\rm{A}}_i}} \wedge {\lambda _i}\overrightarrow u } } }\end{array}} \right.\)
Remarque :
\(\overrightarrow {{M_{eq}}({\rm{G}})} = \sum\limits_i {\overrightarrow {{\rm{G}}{{\rm{A}}_i}} \wedge {\lambda _i}\overrightarrow u = } \overrightarrow 0\) si \(\sum\limits_i {{\lambda _i}\overrightarrow {{\rm{G}}{{\rm{A}}_i}} = } \overrightarrow 0\) car \({\lambda _i} \ne 0\) et \(\overrightarrow u \ne \overrightarrow 0\).