Axe central
L’axe central est le lieu où le torseur peut être réduit en une résultante et un couple, le moment y est minimum, la résultante et le moment y sont colinéaires.
C’est donc l’ensemble des points \({\rm{I}}\) tels que \(\overrightarrow {M\left( {\rm{I}} \right)} = \lambda \overrightarrow R\) où \(\lambda\) est le pas du torseur.
\(\lambda = \frac{{\overrightarrow R .\overrightarrow {M\left( {\rm{A}} \right)} }}{{{{\overrightarrow R }^2}}} = cte\)
Détermination de l’axe central
On cherche un point \({{\rm{I}}^{\rm{*}}}\) tel que \(\overrightarrow {{\rm{A}}{{\rm{I}}^{\rm{*}}}} = \frac{{\overrightarrow R \wedge \overrightarrow {M\left( {\rm{A}} \right)} }}{{{{\overrightarrow R }^2}}}\)
L’axe central est la droite parallèle à la résultante et passant par ce point \({{\rm{I}}^{\rm{*}}}\) : \(\overrightarrow {{\rm{AI}}} = \frac{{\overrightarrow R \wedge \overrightarrow {M\left( {\rm{A}} \right)} }}{{{{\overrightarrow R }^2}}} + \alpha \overrightarrow R.\)
Démonstration
On cherche l’ensemble des points \({\rm{I}}\) tels que \(\overrightarrow {M\left( {\rm{I}} \right)} = \lambda \overrightarrow R\).
Si l’on connait le moment en un point \({\rm{A}}\) alors on peut exprimer celui en \({\rm{I}}\) avec la formule du champ de moments \(\overrightarrow {M\left( {\rm{I}} \right)} = \overrightarrow {M\left( {\rm{A}} \right)} + \overrightarrow {{\rm{IA}}} \wedge \overrightarrow R\).
On a donc la relation suivante \(\overrightarrow {{\rm{AI}}} \wedge \overrightarrow R = \overrightarrow {M\left( {\rm{A}} \right)} - \,\lambda \overrightarrow R \;\).
On peut donc en déduire la position des points \({\rm{I}}\) par rapport au point A, celle-ci étant le résultat de la division vectorielle de \(\left( {\overrightarrow {M\left( {\rm{A}} \right)} - \,\lambda \overrightarrow R \;} \right)\) par \(\overrightarrow R\).
Ce qui donne \(\overrightarrow {{\rm{IA}}} = - \frac{{\overrightarrow R \; \wedge \left( {\overrightarrow {M\left( {\rm{A}} \right)} - \,\lambda \overrightarrow R \;} \right)}}{{{R^2}}} + \alpha \overrightarrow R\)
\(\overrightarrow R \; \wedge \lambda \overrightarrow R = \overrightarrow 0\) car les vecteurs sont colinéaires.
Finalement, \(\overrightarrow {{\rm{IA}}} = - \frac{{\overrightarrow R \; \wedge \overrightarrow {M\left( {\rm{A}} \right)} }}{{{R^2}}} + \alpha \overrightarrow R\)
Soit le point particulier \({{\rm{I}}^{\rm{*}}}\) appartenant à l’axe central tel que \(\overrightarrow {{{\rm{I}}^{\rm{*}}}{\rm{A}}} = - \frac{{\overrightarrow R \; \wedge \overrightarrow {M\left( {\rm{A}} \right)} }}{{{R^2}}}\), c’est-à-dire tel que \(\;\overrightarrow {{{\rm{I}}^{\rm{*}}}{\rm{A}}} \bot \overrightarrow R\).
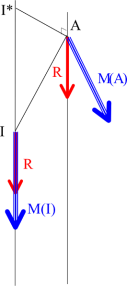
Pas du torseur
On peut obtenir \(\lambda\) en multipliant scalairement \(\;\overrightarrow {{\rm{IA}}} \wedge \overrightarrow R = \lambda \overrightarrow R - \overrightarrow {M\left( {\rm{A}} \right)}\) par \(\overrightarrow R\) :
\(\;\overrightarrow R .\left( {\overrightarrow {{\rm{IA}}} \wedge \overrightarrow R } \right) = \overrightarrow R .\left( {\lambda \overrightarrow R - \overrightarrow {M\left( {\rm{A}} \right)} } \right)\quad \Rightarrow \quad \;0 = \lambda \overrightarrow R .\overrightarrow R - \overrightarrow R .\overrightarrow {M\left( {\rm{A}} \right)}\) car \(\;\overrightarrow R \bot \left( {\overrightarrow {{\rm{IA}}} \wedge \overrightarrow R } \right)\) d’où \(\lambda = \frac{{\overrightarrow R .\overrightarrow {M\left( {\rm{A}} \right)} }}{{{R^2}}}\)