Exercice : Mécanisme planétaire à coulisse [Cinématique]

Mécanisme planétaire à coulisse

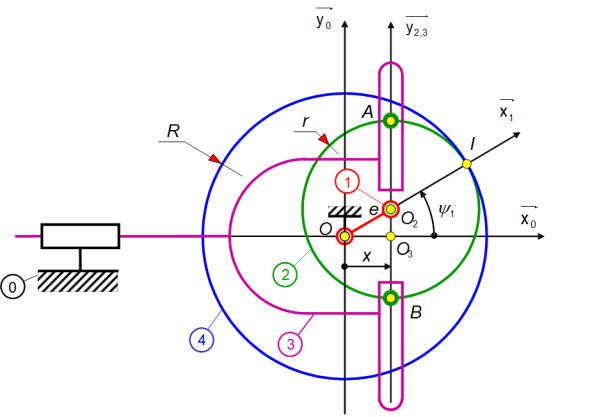
Le mécanisme schématisé figure 1 transforme un mouvement de rotation continue en un mouvement de translation alternative et un mouvement de rotation continue.

Ce mécanisme plan est constitué :

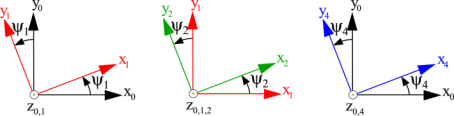
D’une manivelle S₁ en liaison pivot d’axe $(\text{O},\ \overrightarrow{{{z}_{0,1}}})$ avec le bâti $\mathrm{S_0},$ paramétrée ${{\psi }_{1}}=\left( \overrightarrow{{{x}_{0}}},\overrightarrow{{{x}_{1}}} \right).$

D’un pignon S₂ en liaison pivot d’axe $({{\text{O}}_{2}},\overrightarrow{{{z}_{1,2}}})$ avec $\mathrm{S}$, paramétrée ${{\psi }_{2}}=\left( \overrightarrow{{{x}_{1}}},\overrightarrow{{{x}_{2}}} \right)$.

D’une coulisse S₃ en liaison glissière d’axe $(\text{O},\overrightarrow{{{x}_{0,3}}})$ avec $\mathrm{S_0},$ paramétrée $x=\overrightarrow{\text{O}{{\text{O}}_{\text{3}}}}\ .\ \overrightarrow{{{x}_{0,3}}}.$

D’une roue S₄ en liaison pivot d’axe $(\text{O},\overrightarrow{{{z}_{0,4}}})$ avec le bâti $\mathrm{S_0},$ paramétrée ${{\psi }_{4}}=\left( {{\overrightarrow{x}}_{0}},{{\overrightarrow{x}}_{4}} \right).$

Par ailleurs :

deux ergots du pignon $\mathrm{S_2},$ situés en A et B, coulissent dans une rainure d’axe $({{\text{O}}_{3}},\overrightarrow{{{y}_{0,3}}})$ usinée sur $\mathrm{S_3} ;$

la roue $\mathrm{S_4}$ est en contact en I avec le pignon $\mathrm{S_2}$ sur lequel elle roule sans glisser.

Figure 1 : mécanisme planétaire à coulisse

Partie I

Etude du sous ensemble {S1+S2+S3}

Question

Ecrire la ou les équations de liaison traduisant la fermeture de chaîne réalisée par la liaison 2/3.

Solution

La liaison entre 2 et 3 est équivalente à une glissière de direction $\overrightarrow{{{y}_{3,0}}}$, ce qui se traduit par :

pas de translation de 2 par rapport à 3 perpendiculaire à $\overrightarrow{{{y}_{3,0}}}$ :

$\overrightarrow{{{\text{O}}_{\text{2}}}{{\text{O}}_{\text{3}}}}.\overrightarrow{{{x}_{0}}}=0\quad \Rightarrow (\overrightarrow{{{\text{O}}_{\text{2}}}\text{O}}+\overrightarrow{\text{O}{{\text{O}}_{\text{3}}}}).\overrightarrow{{{x}_{0}}}=-e\overrightarrow{{{x}_{1}}}.\overrightarrow{{{x}_{0}}}+x\overrightarrow{{{x}_{0}}}.\overrightarrow{{{x}_{0}}}=0\quad \Rightarrow -e\cos {{\psi }_{1}}+x=0\quad \Rightarrow x=e\cos {{\psi }_{1}}$

pas de rotation de 2 par rapport à 3 autour d’un axe de direction $\overrightarrow{z}$ :

$\overrightarrow{{{y}_{2}}}.\overrightarrow{{{x}_{0}}}=0\ \ \Rightarrow -\sin \left( {{\psi }_{1}}+{{\psi }_{2}} \right)=0\ \ \Rightarrow \ {{\psi }_{2}}=-{{\psi }_{1}}$

Question

Donner la mobilité du système.

Solution

Mobilité du sous-système {1+2+3} = 3 paramètres $(x,{{\psi }_{1}},{{\psi }_{2}})$ – 2 équations = 1.

Question

Préciser la nature du mouvement 3/0 ; donner son torseur distributeur des vitesses en $\mathrm{O_3}$ et l’accélération de $\mathrm{O_3}$.

Solution

Le mouvement de 3 par rapport à 0 est une translation rectiligne de direction $\overrightarrow{{{x}_{0,3}}}$.

Le torseur cinématique du mouvement 3/0 en ${{\text{O}}_{3}}$ est donc

${{\left\{ {{V}_{\text{3/0}}} \right\}}_{{{\text{O}}_{\text{3}}}}}=\left\{ \begin{matrix} \overrightarrow{{{\Omega }_{\text{3/0}}}} \\ \overrightarrow{V\text{(}{{\text{O}}_{\text{3}}}\text{,3/0)}} \\ \end{matrix} \right\}={{\left\{ \begin{matrix} \overrightarrow{0} \\ \dot{x}\overrightarrow{{{x}_{0}}} \\ \end{matrix} \right\}}_{{{\text{O}}_{\text{3}}}}}={{\left\{ \begin{matrix} \overrightarrow{0} \\ -e{{{\dot{\psi }}}_{1}}\sin {{\psi }_{1}}\overrightarrow{{{x}_{0}}} \\ \end{matrix} \right\}}_{{{\text{O}}_{\text{3}}}}}$

$\overrightarrow{V\text{(}{{\text{O}}_{\text{3}}}\text{,3/0)}}=\overrightarrow{V\text{(}{{\text{O}}_{\text{3}}}\text{/0)}}={{\left. \frac{d\overrightarrow{\text{O}{{\text{O}}_{\text{3}}}}}{dt} \right|}_{0}}={{\left. \frac{dx\overrightarrow{{{x}_{0}}}}{dt} \right|}_{0}}=\dot{x}\overrightarrow{{{x}_{0}}}$

L’accélération du point ${{\text{O}}_{3}}$ par rapport à 0 est :

$\overrightarrow{\Gamma \text{(}{{\text{O}}_{\text{3}}}\text{/0)}}={{\left. \frac{d\overrightarrow{V\text{(}{{\text{O}}_{\text{3}}}\text{/0)}}}{dt} \right|}_{0}}=\ddot{x}\overrightarrow{{{x}_{0}}}=-\left( e{{{\ddot{\psi }}}_{1}}\sin {{\psi }_{1}}+e\dot{\psi }_{1}^{2}\cos {{\psi }_{1}} \right)\overrightarrow{{{x}_{0}}}$

Question

Préciser la nature du mouvement 2/0 ; définir la trajectoire de A, le torseur distributeur des vitesses en A et l’accélération de A et $\mathrm{O_2}.$

Solution

Le mouvement de 2 par rapport à 0 est une translation car $(\text{AB})//\overrightarrow{{{y}_{0}}}$.

La trajectoire du point A dans le repère 0 est un cercle de rayon e et de centre C tel que $\overrightarrow{\text{OC}}=\overrightarrow{{{\text{O}}_{2}}\text{A}}=r\overrightarrow{{{y}_{0}}}$ car la trajectoire du point ${{\text{O}}_{2}}$ dans le repère 0 est un cercle de rayon e et de centre O et dans un mouvement de translation tous les points ont des trajectoires similaires.

Le torseur cinématique du mouvement 2/0 en $\text{A}$ est : ${{\left\{ {{V}_{\text{2/0}}} \right\}}_{\text{A}}}=\left\{ \begin{matrix} \overrightarrow{{{\Omega }_{\text{2/0}}}} \\ \overrightarrow{V\text{(A,2/0)}} \\ \end{matrix} \right\}={{\left\{ \begin{matrix} \overrightarrow{0} \\ e{{{\dot{\psi }}}_{1}}\overrightarrow{{{y}_{1}}} \\\end{matrix} \right\}}_{\text{A}}}$

Calcul de la vitesse à partir de sa définition et par dérivation :

$\begin{align} & \overrightarrow{V\text{(A,2/0)}}=\overrightarrow{V\text{(A/0)}}={{\left. \frac{d\overrightarrow{\text{OA}}}{dt} \right|}_{0}}={{\left. \frac{de\overrightarrow{{{x}_{1}}}+r\overrightarrow{{{y}_{0}}}}{dt} \right|}_{0}}={{\left. \frac{de\overrightarrow{{{x}_{1}}}}{dt} \right|}_{0}}+{{\left. \frac{dr\overrightarrow{{{y}_{0}}}}{dt} \right|}_{0}} \\ & ={{\left. \frac{de\overrightarrow{{{x}_{1}}}}{dt} \right|}_{0}}+\overrightarrow{{{\Omega }_{1/0}}}\wedge e\overrightarrow{{{x}_{1}}}\quad (formule\ d\acute{e}rivation\ vectorielle) \\ & =\quad \quad \overrightarrow{0}\quad \ +{{{\dot{\psi }}}_{1}}\overrightarrow{{{z}_{1}}}\wedge e\overrightarrow{{{x}_{1}}}=e{{{\dot{\psi }}}_{1}}\overrightarrow{{{y}_{1}}} \end{align}$

Ou calcul en utilisant la relation de champ des vitesses d’un mouvement et la décomposition des mouvements

$\begin{align} & \overrightarrow{V\text{(A,2/0)}}=\overrightarrow{V\text{(}{{\text{O}}_{\text{2}}}\text{,2/0)}}+\overrightarrow{\text{A}{{\text{O}}_{\text{2}}}}\wedge \overrightarrow{{{\Omega }_{2/0}}} \\ & =\overrightarrow{V\text{(}{{\text{O}}_{\text{2}}}\text{,1/0)}}+r\overrightarrow{{{y}_{0}}}\wedge \overrightarrow{0} \\ & =\overrightarrow{V\text{(O,1/0)}}+\overrightarrow{{{\text{O}}_{\text{2}}}\text{O}}\wedge \overrightarrow{{{\Omega }_{1/0}}} \\ & =\quad \quad \overrightarrow{0}\quad \ +-e\overrightarrow{{{x}_{1}}}\wedge {{{\dot{\psi }}}_{1}}\overrightarrow{{{z}_{1}}}=e{{{\dot{\psi }}}_{1}}\overrightarrow{{{y}_{1}}} \end{align}$

L’accélération de A par rapport à 0 est :

$\overrightarrow{\Gamma \text{(A/0)}}={{\left( \frac{d}{dt}\overrightarrow{V\text{(A/0)}} \right)}_{{{R}_{0}}}}={{\left( \frac{de{{{\dot{\psi }}}_{1}}\overrightarrow{{{y}_{1}}}}{dt} \right)}_{{{R}_{0}}}}={{\left( \frac{de{{{\dot{\psi }}}_{1}}\overrightarrow{{{y}_{1}}}}{dt} \right)}_{{{R}_{1}}}}+\overrightarrow{{{\Omega }_{1/0}}}\wedge e{{\dot{\psi }}_{1}}\overrightarrow{{{y}_{1}}}=e{{\ddot{\psi }}_{1}}\overrightarrow{{{y}_{1}}}-e\dot{\psi }_{1}^{2}\overrightarrow{{{x}_{1}}}$

L’accélération de O₂ par rapport à 0 est :

$\overrightarrow{\Gamma \text{(}{{\text{O}}_{\text{2}}}\text{,2/0)}}=\overrightarrow{\Gamma \text{(A,2/0)}}$ car le mouvement de 2 par rapport à 0 est une translation (tous les points ont la même vitesse dans un mouvement de translation et donc la même accélération).

Question

Préciser la nature du mouvement 2/3 ; donner le torseur des vitesses en A et l’accélération de A et $\mathrm{O_2}$.

Solution

Le mouvement de 2 par rapport à 3 est une translation rectiligne de direction $\overrightarrow{{{y}_{0}}}.$

Le torseur cinématique du mouvement 2/3 en $\text{A}$ est : ${{\left\{ {{V}_{\text{2/3}}} \right\}}_{\text{A}}}=\left\{ \begin{matrix} \overrightarrow{{{\Omega }_{\text{2/3}}}} \\ \overrightarrow{V\text{(A,2/3)}} \\ \end{matrix} \right\}={{\left\{ \begin{matrix} \overrightarrow{0} \\ e{{{\dot{\psi }}}_{1}}\cos {{\psi }_{1}}\overrightarrow{{{y}_{0}}} \\ \end{matrix} \right\}}_{\text{A}}}$

Calcul de la vitesse par composition des 2 mouvements précédents :

$\begin{align} & \overrightarrow{V\text{(A,2/3)}}=\overrightarrow{V\text{(A,2/0)}}-\overrightarrow{V\text{(A,3/0)}} \\ & =e{{{\dot{\psi }}}_{1}}\overrightarrow{{{y}_{1}}}-\dot{x}\overrightarrow{{{x}_{0}}} \\ & =e{{{\dot{\psi }}}_{1}}\overrightarrow{{{y}_{1}}}+e{{{\dot{\psi }}}_{1}}\sin {{\psi }_{1}}\overrightarrow{{{x}_{0}}} \\ & =e{{{\dot{\psi }}}_{1}}\cos {{\psi }_{1}}\overrightarrow{{{y}_{0}}}-e{{{\dot{\psi }}}_{1}}\sin {{\psi }_{1}}\overrightarrow{{{x}_{0}}}+e{{{\dot{\psi }}}_{1}}\sin {{\psi }_{1}}\overrightarrow{{{x}_{0}}} \\ & =e{{{\dot{\psi }}}_{1}}\cos {{\psi }_{1}}\overrightarrow{{{y}_{0}}} \end{align}$

Ou calcul de la vitesse par dérivation :

$\begin{align} & \overrightarrow{V\text{(A,2/3)}}=\overrightarrow{V\text{(A/3)}}-\overrightarrow{V\text{(A/2)}} \\ & =\overrightarrow{V\text{(A/3)}}{{\left. =\frac{d}{dt}\overrightarrow{{{\text{O}}_{\text{3}}}\text{A}} \right|}_{3}} \\ & ={{\left. \frac{d}{dt}(e\sin {{\psi }_{1}}+r)\overrightarrow{{{y}_{3,0}}} \right|}_{3}} \\ & =e{{{\dot{\psi }}}_{1}}\cos {{\psi }_{1}}\overrightarrow{{{y}_{0}}} \end{align}$

L’accélération de A par rapport à 3 est :

$\overrightarrow{\Gamma \text{(A,2/3)}}=\overrightarrow{\Gamma \text{(A/3)}}={{\left( \frac{d}{dt}\overrightarrow{V\text{(A/3)}} \right)}_{{{R}_{3}}}}=e\left( {{{\ddot{\psi }}}_{1}}\cos {{\psi }_{1}}-\dot{\psi }_{1}^{2}\sin {{\psi }_{1}} \right)\overrightarrow{{{y}_{0}}}$

L’accélération de $\mathrm{O_2},$ par rapport à 3 est :

$\overrightarrow{\Gamma \text{(}{{\text{O}}_{\text{2}}}\text{,2/3)}}=\overrightarrow{\Gamma \text{(A,2/3)}}$ car 2/3 est une translation.

Partie II

Etude du mécanisme complet

Question

Ecrire la relation traduisant le non glissement entre 2 et 4 en I et donner la mobilité du système.

Solution

La relation de non-glissement entre le solide 2 et le solide 4 au point I est : $\frac{{{{\dot{\psi }}}_{4}}}{{{{\dot{\psi }}}_{1}}}-=\frac{e}{R}$

$\begin{array}{*{35}{l}} \overrightarrow{V\text{(I,4/2)}}=\overrightarrow{0} & \Rightarrow \ \overrightarrow{V\text{(I,4/0)}}\ -\ \overrightarrow{V\text{(I,2/0)}}=\overrightarrow{0} \\ {} & \begin{align} & \Rightarrow \ \overrightarrow{V\text{(O,4/0)}}\ +\overrightarrow{\text{IO}}\wedge \overrightarrow{{{\Omega }_{4/0}}}-\ \overrightarrow{V\text{(I,2/0)}}=\overrightarrow{0} \\ & \Rightarrow \overrightarrow{0}-R\overrightarrow{{{x}_{1}}}\wedge {{{\dot{\psi }}}_{4}}\overrightarrow{{{z}_{1}}}-e{{{\dot{\psi }}}_{1}}\overrightarrow{{{y}_{1}}}=\overrightarrow{0} \\ & \Rightarrow \left( R{{{\dot{\psi }}}_{4}}-e{{{\dot{\psi }}}_{1}} \right)\overrightarrow{{{y}_{1}}}=\overrightarrow{0} \\ & \Rightarrow R{{{\dot{\psi }}}_{4}}-e{{{\dot{\psi }}}_{1}}=0 \\\end{align} \\\end{array}$

Mobilité du système {1 ; 2 ; 3 ; 4} = 4 paramètres $(x,{{\psi }_{1}},{{\psi }_{2}},{{\psi }_{4}})$ – 3 équations = 1