Tribomètre

Un tribomètre est appareil permettant de mesurer le coefficient de frottement entre deux solides. On peut parfois visualiser ce qui se passe à « l’intérieur » du contact.
Ici, l’étude se fera sur un tribomètre pion – disque (exemple sur photo ci-contre). Grâce à la mesure du déplacement du bras (S2 sur le schéma) lorsque le disque tourne à vitesse constante, on peut connaître le coefficient de frottement de glissement (f) entre le pion (P2) et le disque (S1 sur le schéma).
Le système est constitué d’un bâti S0, référentiel galiléen avec \(\overrightarrow{{{z}_{0}}}\) la verticale descendante, et de 2 solides :
S1, Disque + arbre, en liaison pivot d’axe \((\text{O},\overrightarrow{{{z}_{0,1}}})\) avec S0 et paramétrée \(\psi =(\overrightarrow{{{x}_{0}}},\ \overrightarrow{{{x}_{1}}})\)
S2, Pion + bras, en liaison pivot glissant d’axe \(({{\text{O}}^{*}},\overrightarrow{{{y}_{0,2}}})\) avec S0, de paramètre de rotation \(\theta =(\overrightarrow{{{x}_{0}}},\ \overrightarrow{{{x}_{2}}})\) et de translation \(y=\overrightarrow{\text{O*}{{\text{O}}_{\text{2}}}}.\overrightarrow{{{y}_{0}}}\).
Le contact ponctuel entre S1 et S2 se fait au point P du plan \((O,\ \overrightarrow{{{x}_{0}}},\ \overrightarrow{{{y}_{0}}})\) avec \(\overrightarrow{{{\text{O}}_{\text{2}}}\text{P}}=-a\ \overrightarrow{{{x}_{2}}}\). Cette liaison n’est pas parfaite car on y considère du frottement.
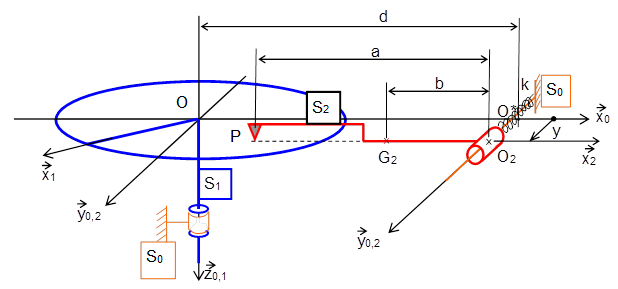
Un ressort de raideur \(k\) est monté entre S2 et S0 de sorte que son action soit nulle pour \(y=0\).
Un couple moteur (Cm) s’exerce sur l’arbre du solide S1 pour maintenir la vitesse de rotation de S1 par rapport à S0 constante (\(\dot{\psi }=\omega =Cste\)).
Données inertielles du solide S1 : masse \({{m}_{1}}\), centre d’inertie \({{\text{G}}_{1}}\in (\text{O},\overrightarrow{{{z}_{1,0}}})\), moment d’inertie \({{C}_{1}}\) par rapport à l’axe \((\text{O},\overrightarrow{{{z}_{1,0}}})\).
Données inertielles du solide S2 : masse \({{m}_{2}}\), centre d’inertie \({{\text{G}}_{2}}\) avec \(\overrightarrow{{{\text{O}}_{\text{2}}}{{\text{G}}_{\text{2}}}}=-b\ \overrightarrow{{{x}_{2}}}\), moment d’inertie \({{A}_{2}}\) par rapport à \(({{\text{G}}_{2}},\overrightarrow{{{y}_{0,2}}})\).
Question
Pour un fonctionnement en régime stationnaire \(\dot{\psi }=\omega =cte\) et \(y={{y}^{*}}=cte\), déterminer le coefficient de frottement \(f\) en fonction de \(y^*\), et le couple moteur nécessaire (\(Cm\)) :
par les théorèmes généraux,
par le théorème de l'énergie cinétique.
Solution
A partir des équations PFD
On obtient l’équation du mouvement du bras (2) en remplaçant les actions mécaniques par leur expression en fonction des paramètres cinématiques dans l’équation de la résultante dynamique suivant \(\overrightarrow y\) :
\({m_2}\ddot y + ky - \frac{f}{{{V_P}}}\frac{b}{a}{m_2}g\left( {\left( {d - a} \right)\dot \psi - \dot y} \right) = 0\)
On obtient l’équation du mouvement du disque (1) en remplaçant les actions mécaniques par leur expression en fonction des paramètres cinématiques dans l’équation du moment dynamique suivant \(\overrightarrow z\) :
\({C_m} + \left( {d - a} \right)\frac{f}{{{V_p}}}\frac{b}{a}{m_2}g\left( {\left( {d - a} \right)\dot \psi - \dot y} \right) + {y^2}\dot \psi \frac{f}{{{V_p}}}\frac{b}{a}{m_2}g - {C_1}\ddot \psi = 0\)
En fonctionnement à régime constant, c'est-à-dire quand \(\dot \psi = \omega = cste\), \(\ddot \psi = 0\) et \(y = {y^*}\), \(\dot y = 0\) et \(\ddot y = 0\)
Les équations précédentes deviennent :
\({C_m} = - f\frac{b}{a}{m_2}g\omega \frac{{{{\left( {d - a} \right)}^2} + {y^2}}}{{V_p^*}} = - f\frac{b}{a}{m_2}g\sqrt {{y^{*2}} + {{\left( {d - a} \right)}^2}}\)
\({y^*} = \frac{f}{{V_p^*}}\frac{b}{a}\frac{{{m_2}}}{k}g\left( {d - a} \right)\omega\)
\(V_p^* = \omega \sqrt {{y^{*2}} + {{\left( {d - a} \right)}^2}}\)
Par le théorème de l'énergie cinétique
On considère l’ensemble du système \(\Sigma = \left\{ {1,2} \right\}\).
Calcul de l’énergie cinétique
\({T_{\Sigma /0}} = {T_{1/0}} + {T_{2/0}}\)
\({T_{1/0}} = \frac{1}{2}{m_1}{\overrightarrow {V({{\rm{G}}_1}/0)} ^2} + \frac{1}{2}\overrightarrow {{\Omega _{1/0}}} \overline{\overline {{I_{{{\rm{G}}_1},1}}}} \overrightarrow {{\Omega _{1/0}}} = 0 + \frac{1}{2}{\left( {\begin{array}{*{20}{c}} 0&0&{\dot \psi } \end{array}} \right)_1}{\left[ {\begin{array}{*{20}{c}} .\\ .\\ 0 \end{array}\begin{array}{*{20}{c}} .\\ .\\ 0 \end{array}\begin{array}{*{20}{c}} 0\\ 0\\ {{C_1}} \end{array}} \right]_1}{\left( {\begin{array}{*{20}{c}} 0\\ 0\\ {\dot \psi } \end{array}} \right)_1} = \frac{1}{2}{C_1}{\dot \psi ^2}\)
\({T_{2/0}} = \frac{1}{2}{m_2}{\overrightarrow {V({{\rm{G}}_2}/0)} ^2} + \frac{1}{2}\overrightarrow {{\Omega _{2/0}}} \overline{\overline {{I_{{{\rm{G}}_2},2}}}} \overrightarrow {{\Omega _{2/0}}} = \frac{1}{2}{m_2}{\dot y^2} + 0\)
\({T_{\Sigma /0}} = \frac{1}{2}{C_1}{\dot \psi ^2} + \frac{1}{2}{m_2}{\dot y^2}\)
Calcul des puissances
Actions extérieures
Action de 0 sur 1 (liaison pivot parfaite)
\({P_{0 \to 1/0}} = \overrightarrow {{F_{0 \to 1}}} .\overrightarrow {V({{\rm{O}}_1}/0)} + \overrightarrow {{M_{0 \to 1}}({{\rm{O}}_1})} \overrightarrow {{\Omega _{1/0}}} = 0\)
Action de 0 sur 2 (liaison pivot glissante parfaite)
\({P_{0 \to 2/0}} = \overrightarrow {{F_{0 \to 2}}} .\overrightarrow {V({{\rm{O}}_2}/0)} + \overrightarrow {{M_{0 \to 2}}({{\rm{O}}_2})} \overrightarrow {{\Omega _{2/0}}} = 0\)
Couple moteur sur 1
\({P_{m \to 1/0}} = {C_m}\overrightarrow {{z_{0,1}}} .\overrightarrow {{\Omega _{1/0}}} = {C_m}\overrightarrow {{z_{0,1}}} .\dot \psi \overrightarrow {{z_{0,1}}} . = {C_m}\dot \psi\)
Ressort sur 2
\({P_{r \to 2/0}} = - ky\overrightarrow {{y_{0,2}}} .\overrightarrow {V({{\rm{O}}_2}/0)} + \overrightarrow 0 .\overrightarrow {{\Omega _{2/0}}} = - ky\dot y\)
Pesanteur sur 1 et 2 (=0 car les altitudes des centres de masse sont constantes)
\({P_{pes \to \Sigma /0}} = {P_{pes \to 1/0}} + {P_{pes \to 2/0}} = {m_1}g\overrightarrow {{z_0}} .\overrightarrow {V({{\rm{G}}_1}/0)} + {m_2}g\overrightarrow {{z_0}} .\overrightarrow {V({{\rm{G}}_2}/0)} = 0\)
Remarque :
Pour le ressort et la pesanteur, on aurait pu calculer à partir des fonctions de force.
Actions intérieures au système \(\Sigma = \left\{ {1,2} \right\}\)
Liaison ponctuelle imparfaite entre 1 et 2 (actions de 1 sur 2 et de 2 sur 1)
\(\begin{array}{c} {P_{L12/0}} = \overrightarrow {{F_{2 \to 1}}} .\overrightarrow {V({{\rm{P}}_2},1/2)} + \overrightarrow {{M_{2 \to 1}}({{\rm{P}}_2})} \overrightarrow {{\Omega _{1/2}}} \\ = {\left( \begin{array}{l} {X_{21}}\\ {Y_{21}}\\ {Z_{21}} \end{array} \right)_0}.{\left( \begin{array}{l} - y\dot \psi \\ \left( {d - a} \right)\dot \psi - \dot y\\ 0 \end{array} \right)_0} + \overrightarrow 0 .\overrightarrow {{\Omega _{1/2}}} \\ = - y\dot \psi {X_{21}} + \left( {\left( {d - a} \right)\dot \psi - \dot y} \right){Y_{21}} \end{array}\)
Théorème de l’énergie cinétique
\(\frac{{d{T_{\Sigma /0}}}}{{dt}} = {P_{ext \to \Sigma /0}} + {P_{int}}\)
\(\frac{d}{{dt}}\left( {\frac{1}{2}{C_1}{{\dot \psi }^2} + \frac{1}{2}{m_2}{{\dot y}^2}} \right) = {C_m}\dot \psi - ky\dot y - y\dot \psi {X_{21}} + \left( {\left( {d - a} \right)\dot \psi - \dot y} \right){Y_{21}}\)
\({C_1}\dot \psi \ddot \psi + {m_2}\dot y\ddot y = {C_m}\dot \psi - ky\dot y - y\dot \psi {X_{21}} + \left( {\left( {d - a} \right)\dot \psi - \dot y} \right){Y_{21}}\)
En fonctionnement à régime stationnaire, c'est-à-dire quand \(\dot \psi = \omega = cste\), \(\ddot \psi = 0\) et \(y = {y^*}\), \(\dot y = 0\) et \(\ddot y = 0\)
\(0 = {C_m}\omega - {y^*}\omega {X_{21}} + \left( {d - a} \right)\omega {Y_{21}}\)
\({C_m} = {y^*}{X_{21}} - \left( {d - a} \right){Y_{21}}\)
On retrouve l’équation du PFD donc on retrouve la même valeur du couple moteur.