Cylindre roulant
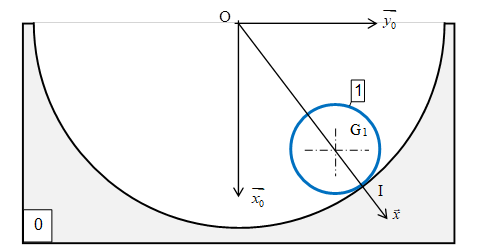
Un cylindre S1 de révolution, plein homogène de rayon r et de masse m, peut rouler sans glisser dans un cylindre S0, creux de rayon R. Les axes des deux cylindres sont horizontaux et parallèles.
Le mouvement de S1/S0 est défini par :
\(\phi =(\overrightarrow{{{x}_{0}}},\overrightarrow{x})\) paramétrant l’orientation du vecteur \(\overrightarrow{\text{O}{{\text{G}}_{1}}}\) par rapport à \(\overrightarrow{{{x}_{0}}}\) ;
\(\theta =(\overrightarrow{{{x}_{0}}},\overrightarrow{{{x}_{1}}})\) paramétrant la rotation propre de S1 par rapport à S0.
Question
Appliquer le théorème de l’énergie cinétique au solide 1.
Solution
Calcul de l’énergie cinétique
L’énergie cinétique du cylindre est :
\(\begin{array}{c} {T_{1/0}} = \frac{1}{2}m{\overrightarrow {V({{\rm{G}}_1}/0)} ^2} + \frac{1}{2}\overrightarrow {{\Omega _{1/0}}} \overline{\overline {{I_{{{\rm{G}}_1},1}}}} \overrightarrow {{\Omega _{1/0}}} \\ = \frac{1}{2}m{\left( {\left( {R - r} \right)\dot \varphi \overrightarrow y } \right)^2} + \frac{1}{2}{\left( {\begin{array}{*{20}{c}} 0&0&{\dot \theta } \end{array}} \right)_{0,1}}{\left[ {\begin{array}{*{20}{c}} .\\ .\\ 0 \end{array}\begin{array}{*{20}{c}} .\\ .\\ 0 \end{array}\begin{array}{*{20}{c}} 0\\ 0\\ {\frac{{m{r^2}}}{2}} \end{array}} \right]_{0,1}}{\left( {\begin{array}{*{20}{c}} 0\\ 0\\ {\dot \theta } \end{array}} \right)_{0,1}}\\ = \frac{1}{2}m{\left( {R - r} \right)^2}{{\dot \varphi }^2} + \frac{1}{2}\frac{{m{r^2}}}{2}{{\dot \theta }^2} \end{array}\)
On a l’équation de liaison de roulement sans glissement : \(\left( {R - r} \right)\dot \varphi + r\dot \theta = 0\)
Donc \({T_{1/0}} = \frac{3}{4}m{\left( {R - r} \right)^2}{\dot \varphi ^2}\)
Calcul des puissances
Puissance développée par la pesanteur
\({P_{pes \to 1/0}} = mg\overrightarrow {{x_0}} .\overrightarrow {V({{\rm{G}}_1}/0)} = mg\overrightarrow {{x_0}} .\left( {R - r} \right)\dot \varphi \overrightarrow y = - \sin \varphi \,mg\left( {R - r} \right)\dot \varphi\)
Fonction de force de pesanteur : \({U_{pes}} = mg{x_{{\rm{0}}{{\rm{G}}_1}}} + cte = mg\left( {R - r} \right)\cos \varphi \, + cte\)
\({P_{pes \to 1/0}} = \frac{{d{U_{pes}}}}{{dt}} = - mg\left( {R - r} \right)\dot \varphi \sin \varphi \,\)
Puissance développée par le contact (roulement sans glissement) :
\({P_{0 \to 1/0}} = \overrightarrow {{F_{0 \to 1}}} .\overrightarrow {V({\rm{I,1}}/0)} + \overrightarrow {{M_{0 \to 1}}({\rm{I}})} .\overrightarrow {{\Omega _{1/0}}} = \overrightarrow {{F_{0 \to 1}}} .\overrightarrow 0 + \overrightarrow 0 .\overrightarrow {{\Omega _{1/0}}} = 0\)
Théorème de l’énergie cinétique
\(\frac{{d{T_{\Sigma /0}}}}{{dt}} = {P_{ext \to \Sigma /0}} + {P_{int}} \quad \Rightarrow \quad \frac{3}{2}m{\left( {R - r} \right)^2}\dot \varphi \ddot \varphi = - mg\left( {R - r} \right)\dot \varphi \sin \varphi \, \quad \Rightarrow \quad \frac{3}{2}\left( {R - r} \right)\ddot \varphi + g\sin \varphi \, = 0\)
Remarque :
Seules les actions dérivant de fonction de force travaillent, on peut donc écrire le théorème sous sa forme intégrée :
\({T_{\Sigma /0}} - {U_{pes}} = cte \quad \Rightarrow \quad \frac{3}{4}m{\left( {R - r} \right)^2}{\dot \varphi ^2} + mg\left( {R - r} \right)\cos \varphi \, = cte \quad \Rightarrow \quad \frac{3}{4}\left( {R - r} \right){\dot \varphi ^2} + g\cos \varphi \, = cte\)