Etude d’un manège
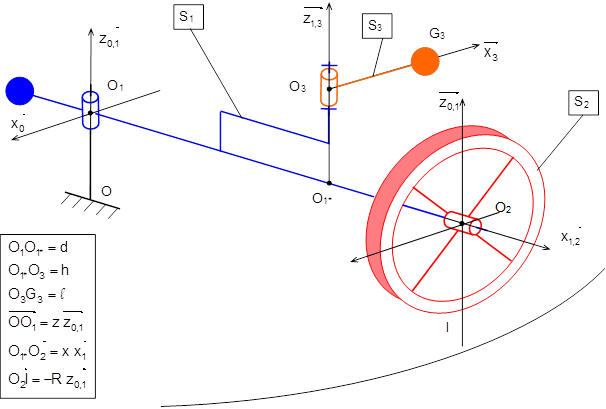
Le système, schématisé sur la figure, est constitué :
d’un bâti S0, auquel est lié un repère \({{R}_{0}}(\text{O},\,\overrightarrow{{{x}_{0}}},\ \overrightarrow{{{y}_{0}}},\ \overrightarrow{{{z}_{0}}})\) galiléen où \(\overrightarrow{{{z}_{0}}}\) est vertical ascendant.
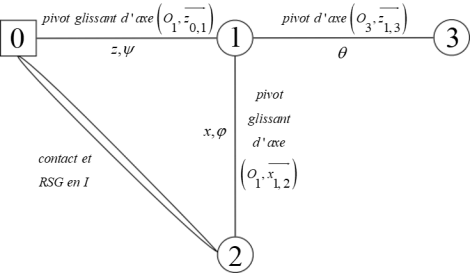
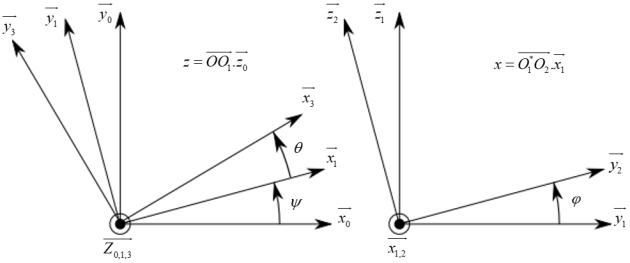
d’un solide S1 en liaison pivot glissant d’axe \((\text{O},\ \overrightarrow{{{z}_{0,1}}})\) avec S0, paramétrée \(\psi =(\overrightarrow{{{x}_{0}}},\ \overrightarrow{{{x}_{1}}})\) et \(z=\overrightarrow{\text{O}{{\text{O}}_{\text{1}}}}.\overrightarrow{{{z}_{0,1}}}\)
d’une roue S2 en liaison pivot glissant d’axe \(({{\text{O}}_{1}},\ \overrightarrow{{{x}_{1,2}}})\) avec S1, paramétrée \(\phi =(\overrightarrow{{{y}_{1}}},\ \overrightarrow{{{y}_{2}}})\) et \(x=\overrightarrow{{{\text{O}}_{\text{1*}}}{{\text{O}}_{\text{2}}}}.\overrightarrow{{{x}_{1}}}\)
d’une nacelle S3 en liaison pivot d’axe \(({{\text{O}}_{3}},\ \overrightarrow{{{z}_{1,3}}})\) avec S1, paramétrée \(\theta =(\overrightarrow{{{x}_{1}}},\ \overrightarrow{{{x}_{3}}})\)
Un moteur, monté entre S0 et S1, exerce sur S1 un couple \({{C}_{m}}\ \overrightarrow{{{z}_{0,1}}}.\)
Un second moteur, monté entre S1 et S3, exerce sur S3 un couple \(C{{'}_{m}}\ \overrightarrow{{{z}_{0,1,3}}}.\)
Un ressort de traction-compression, de raideur \(k\) et dont l’action s’annule avec \(x,\) est placé entre S1 et S2.
La roue S2 de rayon R est en contact en I avec le plan \((\text{O},\,\overrightarrow{{{x}_{0}}},\ \overrightarrow{{{y}_{0}}})\) et est munie d’un pneumatique de paramètre de dérive D (constante donnée).
La liaison S0/S2 est caractérisée :
du point de vue cinématique, par un non glissement longitudinal : \(\overrightarrow{V(\,\text{I},\,2/0)}.\overrightarrow{{{y}_{1}}}=0\)
du point de vue dynamique par son torseur :
\(\left\{ F{{\ }_{0\to 2}} \right\}=\left\{ \begin{array}{*{35}{l}} \overrightarrow{{{F}_{0\to 2}}}=-D\ \delta \ \overrightarrow{{{x}_{1}}}+{{Y}_{02}}\ \overrightarrow{{{y}_{1}}}\ +{{Z}_{02}}\ \overrightarrow{{{z}_{1}}}\ \\ \overrightarrow{{{M}_{0\to 2}}}(\text{I})=\overrightarrow{0} \\ \end{array} \right\}\)
où la composante transversale de l’action de contact est rattachée à la dérive du pneumatique avec \(D\) la rigidité de dérive et \(\delta\) l’angle de dérive, qui est l’angle que fait la vitesse du point géométrique de contact I dans son mouvement par rapport à S0 avec l’intersection du plan de la roue \(({{\text{O}}_{2}},\overrightarrow{{{y}_{2}}},\ \overrightarrow{{{z}_{2}}})\) et du plan \((\text{I},\overrightarrow{{{x}_{1}}},\ \overrightarrow{{{y}_{1}}})\) tangent à la roue en I : \(\delta =\arctan \frac{\overrightarrow{V(\,\text{I}/0)}.\overrightarrow{{{x}_{1}}}}{\overrightarrow{V(\,\text{I}/0)}.\overrightarrow{{{y}_{1}}}}\)
Données inertielles
Solide S1 : masse m1, centre d’inertie O1, tenseur d’inertie \(\overline{\overline{{{I}_{{{\text{O}}_{\text{1}}},1}}}}={{\left[ \begin{array}{*{35}{l}} {{A}_{\text{1}}} & 0 & 0 \\0 & {{B}_{\text{1}}} & 0 \\ 0 & 0 & {{C}_{\text{1}}} \\ \end{array} \right]}_{1}}\)
Solide S2 : masse m2, centre d’inertie O2, tenseur d’inertie \(\overline{\overline{{{I}_{{{\text{O}}_{\text{2}}},2}}}}={{\left[ \begin{array}{*{35}{l}} {{A}_{\text{2}}} & 0 & 0 \\ 0 & {{B}_{\text{2}}} & 0 \\ 0 & 0 & {{B}_{\text{2}}} \\ \end{array} \right]}_{2}}\)
Solide S3 : masse ponctuelle m3 en G3
Par ailleurs, on donne sous forme intrinsèque l’accélération du point G3 dans son mouvement par rapport à S0 : \(\overrightarrow{\Gamma ({{\text{G}}_{3}}/0)}=-d{{\dot{\psi }}^{2}}\overrightarrow{{{x}_{1}}}+d\ddot{\psi }\overrightarrow{{{y}_{1}}}-l{{(\dot{\theta }+\dot{\psi })}^{2}}\overrightarrow{{{x}_{3}}}+l(\ddot{\theta }+\ddot{\psi })\overrightarrow{{{y}_{3}}}\)
Question
Ecrire les équations de liaison traduisant en I : le contact et le non glissement longitudinal.
Solution
Bilan global
| Inconnues | 22 | Equations | 22 |
Cinématique | x, z, \(\psi,\) \(\phi,\) \(\theta\) | 5 | Equations de liaison |
|
|
|
| 1 | |
|
|
| 1 | |
Dynamique |
| 4 | PFD (3 solides en 3D) | 18 |
| 4 |
|
| |
| 5 | Lois de comportement |
| |
| 3 |
| 1 | |
| 1 |
| 1 |
Mobilité
m = n inconnues cinématiques – l équations de liaison
m = 5 – 2 = 3
L’équation de liaison traduisant le contact entre 2 et 0 en I est :
\(\overrightarrow{\text{OI}}.\overrightarrow{{{z}_{0,1,3}}}=0\quad \Rightarrow \quad z=R \quad(1)\)
On considère par la suite que le contact est permanent c’est à dire que \(z=R\) donc \(\dot{z}=\ddot{z}=0\)
L’équation traduisant le roulement sans glissement de 2 par rapport à 0 en I est :
\(\overrightarrow{V\left( \text{I,2/0} \right)}.\overrightarrow{{{y}_{1}}}=0\)
avec
\(\begin{align} & \overrightarrow{V\left( \text{I,2/0} \right)}=\overrightarrow{V\left( {{\text{O}}_{\text{2}}}\text{,2/0} \right)}+\overrightarrow{\text{I}{{\text{O}}_{\text{2}}}}\wedge \overrightarrow{{{\Omega }_{2/0}}} \\ & =\overrightarrow{V\left( {{\text{O}}_{\text{2}}}\text{,2/1} \right)}+\overrightarrow{V\left( {{\text{O}}_{\text{2}}}\text{,1/0} \right)}+\overrightarrow{\text{I}{{\text{O}}_{\text{2}}}}\wedge \overrightarrow{{{\Omega }_{2/0}}} \\ & =\overrightarrow{V\left( {{\text{O}}_{\text{2}}}\text{,2/1} \right)}+\overrightarrow{V\left( {{\text{O}}_{\text{1}}}\text{,1/0} \right)}+\overrightarrow{{{\text{O}}_{\text{2}}}{{\text{O}}_{\text{1}}}}\wedge \overrightarrow{{{\Omega }_{1/0}}}+\overrightarrow{\text{I}{{\text{O}}_{\text{2}}}}\wedge \left( \overrightarrow{{{\Omega }_{2/1}}}+\overrightarrow{{{\Omega }_{1/0}}} \right) \\ & =\dot{x}\overrightarrow{{{x}_{1,2}}}+\dot{z}\overrightarrow{{{z}_{0,1}}}-\left( d+x \right)\overrightarrow{{{x}_{1,2}}}\wedge \dot{\psi }\overrightarrow{{{z}_{0,1}}}+R\overrightarrow{{{z}_{0,1}}}\wedge \left( \dot{\phi }\overrightarrow{{{x}_{1,2}}}+\dot{\psi }\overrightarrow{{{z}_{0,1}}} \right) \\ & =\dot{x}\overrightarrow{{{x}_{1}}}+\left[ \left( d+x \right)\dot{\psi }+R\dot{\phi } \right]\overrightarrow{{{y}_{1}}} \end{align}\)
d'où \(\left( d+x \right)\dot{\psi }+R\dot{\phi }=0 \quad(2)\)
Question
Effectuer la mise équations permettant d’obtenir les équations de mouvement.
Solution
Système minimum
| Inconnues | 9 | Equations | 9 |
Cinématique | x, z, \(\psi\), \(\phi\), \(\theta\) | 5 | Equations de liaison |
|
|
|
| 1 | |
|
|
| 1 | |
Dynamique |
\(X_{02}, Y_{02}, Z_{02}\) | 3 | TMD appliqué à S3 en O3 sur \(\overrightarrow{z_{0,1,3}}\) | 1 |
| TRD appliqué à S2 sur \(\overrightarrow{x_1}\) | 1 | ||
| 1 | TMD appliqué à S2 en O2 sur \(\overrightarrow{x_1}\) | 1 | |
|
| TRD appliqué à S={S1+S2+S3} sur \(\overrightarrow{z_{0,1,3}}\) | 1 | |
|
| TMD appliqué à S={S1+S2+S3} en O1 en sur \(\overrightarrow{z_{0,1,3}}\) | 1 | |
|
| Lois de comportement |
| |
|
|
| 1 | |
|
|
| 1 |
Loi de comportement du ressort
\(\overrightarrow{{{F}_{R1\to 2}}}=-k\left( l-{{l}_{0}} \right)\frac{\overrightarrow{{{\text{O}}_{\text{1*}}}{{\text{O}}_{\text{2}}}}}{\left\| \overrightarrow{{{\text{O}}_{\text{1*}}}{{\text{O}}_{\text{2}}}} \right\|}=-k\left( l-{{l}_{0}} \right)\overrightarrow{{{x}_{1}}}\)
Dans l’énoncé, il est dit que l'action du ressort s’annule avec \(x\) donc \(l-{{l}_{0}}=x.\)
\(\overrightarrow{{{F}_{R1\to 2}}}=-kx\overrightarrow{{{x}_{1}}}={{F}_{R}}\overrightarrow{{{x}_{1}}} \quad (3)\)
Loi de comportement de dérive du pneumatique
\({{X}_{02}}=\overrightarrow{{{F}_{0\to 2}}}.\overrightarrow{{{x}_{1}}}=D\delta\) avec \(D=cste\) la rigidité de dérive et \(\delta =-\arctan \left( \frac{\overrightarrow{V\left( \text{I}/0 \right)}.\overrightarrow{{{x}_{1}}}}{\overrightarrow{V\left( \text{I}/0 \right)}.\overrightarrow{{{y}_{1}}}} \right)\) l’angle de dérive
\(\overrightarrow{V\left( \text{I/0} \right)}\) est la vitesse du point géométrique I par rapport au référentiel galiléen \({{R}_{0}}.\)
\(\overrightarrow{V\left( \text{I/0} \right)}={{\left( \frac{d\overrightarrow{\text{OI}}}{dt} \right)}_{{{R}_{0}}}}=\dot{x}\overrightarrow{{{x}_{1}}}+\left( d+x \right){{\left( \frac{d\overrightarrow{{{x}_{1}}}}{dt} \right)}_{{{R}_{0}}}}=\dot{x}\overrightarrow{{{x}_{1}}}+\left( d+x \right)\dot{\psi }\overrightarrow{{{y}_{1}}}\)
Ou on peut aussi remarquer que le point I est fixe par rapport au point \({{\text{O}}_{\text{2}}}\) d’où \(\overrightarrow{V\left( \text{I/0} \right)}=\overrightarrow{V\left( {{\text{O}}_{\text{2}}}\text{/0} \right)}=\overrightarrow{V\left( {{\text{O}}_{\text{2}}}\text{,2/0} \right)}\)
La loi de dérive, suivant \(\overrightarrow{{{x}_{1}}},\) se traduit donc par la relation : \(\overrightarrow{{{F}_{0\to 2}}}.\overrightarrow{{{x}_{1}}}={{X}_{02}}=-D\arctan \left( \frac{{\dot{x}}}{\left( d+x \right)\dot{\psi }} \right) \quad (4)\)
TMD appliqué à la nacelle (3)
en \({{\text{O}}_{\text{3}}}\) suivant \(\overrightarrow{{{z}_{0,1,3}}}.\)
Les actions mécaniques extérieures s’exerçant sur la nacelle (3) sont :
l’action de pesanteur : \(\overrightarrow{{{M}_{pes\to 3}}\left( {{\text{O}}_{3}} \right)}.\overrightarrow{{{z}_{0,1}}}=0\) car la résultante est colinéaire à la direction de projection
l’action de liaison de 1 sur 3 : \(\overrightarrow{{{M}_{1\to 3}}\left( {{\text{O}}_{3}} \right)}.\overrightarrow{{{z}_{1}}}=0\)
le couple du moteur : \(\overrightarrow{{{M}_{m'\to 3}}\left( {{\text{O}}_{3}} \right)}.\overrightarrow{{{z}_{1}}}=C_{m}^{'}\)
La nacelle (3) est considérée comme une masse ponctuelle en \({{\text{G}}_{\text{3}}}\) (la matrice d’inertie est donc nulle en ce point), son moment dynamique en \({{\text{G}}_{\text{3}}}\) par rapport au bâti (0) est donc nul : \(\overrightarrow{\delta ({{\text{G}}_{\text{3}}},3/0)}=\frac{d}{dt}\overrightarrow{\sigma ({{\text{G}}_{\text{3}}},3/0)}=\overrightarrow{0}\) car \(\overrightarrow{\sigma ({{\text{G}}_{\text{3}}},3/0)}=\overline{\overline{{{I}_{{{\text{G}}_{\text{3}}},3}}}}.\overrightarrow{{{\Omega }_{3/0}}}=\left[ 0 \right]\overrightarrow{{{\Omega }_{3/0}}}=\overrightarrow{0}\)
La formule du transport du moment dynamique nous donne :
\(\begin{align} & \overrightarrow{\delta \left( {{\text{O}}_{\text{3}}},3/0 \right)}=\overrightarrow{\delta ({{\text{G}}_{\text{3}}},3/0)}+\overrightarrow{{{\text{O}}_{\text{3}}} {{\text{G}}_{\text{3}}}}\wedge {{m}_{3}}\overrightarrow{\Gamma ({{\text{G}}_{\text{3}}},3/0)} \\ & =\overrightarrow{0}+{{\left( \begin{matrix} l \\ 0 \\ 0 \\ \end{matrix} \right)}_{{{R}_{3}}}}\wedge {{m}_{3}}{{\left( \begin{array}{*{35}{l}} -d{{{\dot{\psi }}}^{2}}\cos \theta +d\ddot{\psi }\sin \theta -l{{\left( \dot{\theta }+\dot{\psi } \right)}^{2}} \\ d{{{\dot{\psi }}}^{2}}\sin \theta +d\ddot{\psi }cos\theta +l\left( \ddot{\theta }+\ddot{\psi } \right) \\ 0 \\ \end{array} \right)}_{{{R}_{3}}}} \\ & ={{m}_{3}}l\left[ d\left( {{{\dot{\psi }}}^{2}}sin\theta +\ddot{\psi }cos\theta \right)+l\left( \ddot{\theta }+\ddot{\psi } \right) \right]\overrightarrow{{{z}_{3}}} \end{align}\)
Le théorème du moment dynamique appliqué à la nacelle (3) en \({{\text{O}}_{\text{3}}}\) en projection sur l'axe \(\overrightarrow{{{z}_{0,1,3}}}\) se traduit par : \(C_{m}^{'}={{m}_{3}}l\left[ d\left( {{{\dot{\psi }}}^{2}}sin\theta +\ddot{\psi }cos\theta \right)+l\left( \ddot{\theta }+\ddot{\psi } \right) \right] \quad (5)\)
TRD et TMD
En \({{\text{O}}_{\text{2}}}\) de la roue (2) suivant \(\overrightarrow{{{x}_{1}}}.\)
Les actions mécaniques extérieures s’exerçant sur la roue (2) sont :
l’action de pesanteur : \(\overrightarrow{{{F}_{pes\to 2}}}.\overrightarrow{{{x}_{1}}}=0\) et \(\overrightarrow{{{M}_{pes\to 2}}\left( {{\text{O}}_{\text{2}}} \right)}.\overrightarrow{{{x}_{1}}}=0\)
l’action de liaison de 1 sur 2 : \(\overrightarrow{{{F}_{1\to 2}}}.\overrightarrow{{{x}_{1}}}=0\) et \(\overrightarrow{{{M}_{1\to 2}}\left( {{\text{O}}_{\text{2}}} \right)}.\overrightarrow{{{x}_{1}}}=0\)
l’action du ressort : \(\overrightarrow{{{F}_{\operatorname{Re}ssort\to 2}}}.\overrightarrow{{{x}_{1}}}={{F}_{R}}\) et \(\overrightarrow{{{M}_{R\to 2}}\left( {{\text{O}}_{\text{2}}} \right)}.\overrightarrow{{{x}_{1}}}=0\)
l’action du sol sur le pneumatique : \(\overrightarrow{{{F}_{0\to 2}}}.\overrightarrow{{{x}_{1}}}={{X}_{02}}\) et \(\overrightarrow{{{M}_{0\to 2}}\left( {{\text{O}}_{\text{2}}} \right)}.\overrightarrow{{{x}_{1}}}=\left( \overrightarrow{{{M}_{0\to 2}}\left( \text{I} \right)}-R\overrightarrow{{{z}_{01}}}\wedge \overrightarrow{{{F}_{0\to 2}}} \right).\overrightarrow{{{x}_{1}}}=R{{Y}_{02}}\)
La résultante dynamique de la roue (2) par rapport au sol (0) est :
\(\begin{align} & \overrightarrow{D\left( 2/0 \right)}={{m}_{2}}\overrightarrow{\Gamma \left( {{\text{O}}_{\text{2}}},2/0 \right)} \\ & ={{m}_{2}}{{\left( \frac{{{d}^{2}}} {d{{t}^{2}}}\overrightarrow{\text{O}{{\text{O}}_{\text{2}}}} \right)}_{{{R}_{0}}}} \\ & ={{m}_{2}}{{\left( \frac{{{d}^{2}}}{d{{t}^{2}}}\left( z\overrightarrow{{{z}_{0,1}}}+\left( d+x \right)\overrightarrow{{{x}_{1}}} \right) \right)}_{{{R}_{0}}}} \\ & ={{m}_{2}}\ddot{z}\overrightarrow{{{z}_{0,1}}}+{{m}_{2}}{{\left( \frac{d}{dt}\left( \dot{x}\overrightarrow{{{x}_{1}}}+\left( d+x \right)\dot{\psi }\overrightarrow{{{y}_{1}}} \right) \right)}_{{{R}_{0}}}} \\ & ={{m}_{2}}\left( \ddot{x}\overrightarrow{{{x}_{1}}}+\dot{x}\dot{\psi }\overrightarrow{{{y}_{1}}}+\left( \dot{x}\dot{\psi }+\left( d+x \right)\ddot{\psi } \right)\overrightarrow{{{y}_{1}}}-\left( d+x \right){{{\dot{\psi }}}^{2}}\overrightarrow{{{x}_{1}}} \right) \\ & ={{m}_{2}}\left( \ddot{x}-\left( d+x \right){{{\dot{\psi }}}^{2}} \right)\overrightarrow{{{x}_{1}}}+{{m}_{2}}\left( 2\dot{x}\dot{\psi }+\left( d+x \right)\ddot{\psi } \right)\overrightarrow{{{y}_{1}}} \end{align}\)
Le théorème de la résultante dynamique appliqué à la roue (2) en projection sur l'axe \(\overrightarrow{{{x}_{1}}}\) donne :
\({{F}_{R}}+{{X}_{02}}={{m}_{2}}\left( \ddot{x}-\left( d+x \right){{{\dot{\psi }}}^{2}} \right) \quad (6)\)
Le moment dynamique de la roue (2) par rapport au sol (0) en \({{\text{O}}_{\text{2}}}\) (son centre d’inertie) est :
\(\begin{align} & \overrightarrow{\delta ({{\text{O}}_{\text{2}}},2/0)}=\frac{d}{dt}{{\left( \overrightarrow{\sigma ({{\text{O}}_{\text{2}}},2/0)} \right)}_{{{R}_{0}}}} \\ & =\frac{d}{dt}{{\left( \overline{\overline{{{I}_{{{\text{O}}_{\text{2}}},2}}}}.\overrightarrow{{{\Omega }_{2/0}}} \right)}_{{{R}_{0}}}} \\ & =\frac{d}{dt}{{\left( {{\left[ \begin{matrix} {{A}_{2}} & 0 & 0 \\ 0 & {{B}_{2}} & 0 \\ 0 & 0 & {{B}_{2}} \\ \end{matrix} \right]}_{{{R}_{1}}}}{{\left( \begin{matrix} {\dot{\phi }} \\ 0 \\ {\dot{\psi }} \\ \end{matrix} \right)}_{{{R}_{1}}}} \right)}_{{{R}_{0}}}} \\ & =\frac{d}{dt}{{\left( {{A}_{2}}\dot{\phi }\overrightarrow{{{x}_{1}}}+{{B}_{2}}\dot{\psi }\overrightarrow{{{z}_{1,0}}} \right)}_{{{R}_{0}}}} \\ & ={{A}_{2}}\ddot{\phi }\overrightarrow{{{x}_{1}}}+{{A}_{2}}\dot{\phi }\dot{\psi }\overrightarrow{{{y}_{1}}}+{{B}_{2}}\ddot{\psi }\overrightarrow{{{z}_{1,0}}} \end{align}\)
Remarque :
La roue est considérée comme un solide de révolution, sa matrice d’inertie est donc la même dans les bases \({{R}_{2}}\) et \({{R}_{1}}\) (axe de révolution = axe de rotation).
Le théorème du moment dynamique appliqué à la roue (2) en \({{\text{O}}_{\text{2}}}\) en projection sur l'axe \(\overrightarrow{{{x}_{1}}}\) :
\(R{{Y}_{02}}={{A}_{2}}\ddot{\phi } \quad (7)\)
TRD
Appliqué à \(S=\left\{ 1+2+3 \right\}\) sur \(\overrightarrow{{{z}_{0,1,3}}}\)
Les actions mécaniques extérieures s’exerçant sur cet ensemble sont :
l’action de la pesanteur sur 1, 2 et 3 : \(\overrightarrow{{{F}_{pes\to S}}}.\overrightarrow{{{z}_{0}}}=-\left( {{m}_{1}}+{{m}_{2}}+{{m}_{3}} \right)g\) et \(\overrightarrow{{{M}_{pes\to S}}\left( {{\text{O}}_{\text{1}}} \right)}.\overrightarrow{{{z}_{0}}}=0\)
l’action de liaison de 0 sur 1 : \(\overrightarrow{{{F}_{0\to 1}}}.\overrightarrow{{{z}_{0}}}=0\) et \(\overrightarrow{{{M}_{0\to 1}}\left( {{\text{O}}_{\text{1}}} \right)}.\overrightarrow{{{z}_{0}}}=0\)
l’action de liaison de 0 sur 2 : \(\overrightarrow{{{F}_{0\to 2}}}.\overrightarrow{{{z}_{0}}}={{Z}_{02}}\) et \(\overrightarrow{{{M}_{0\to 2}}\left( {{\text{O}}_{\text{1}}} \right)}.\overrightarrow{{{z}_{0}}}=\left( d+x \right){{Y}_{02}}\)
le couple du moteur : \(\overrightarrow{{{F}_{moteur\to 1}}}.\overrightarrow{{{z}_{0}}}=0\) et \(\overrightarrow{{{M}_{moteur\to 1}}\left( {{\text{O}}_{\text{1}}} \right)}.\overrightarrow{{{z}_{0}}}={{C}_{m}}\)
La résultante dynamique de l’ensemble \(S\) est égale à la somme des résultantes dynamiques des éléments qui le composent :
\(\overrightarrow{D_{S/0}^{{}}}=\overrightarrow{D_{1/0}^{{}}}+\overrightarrow{D_{2/0}^{{}}}+\overrightarrow{D_{3/0}^{{}}}={{m}_{1}}\overrightarrow{\Gamma \left( {{\text{O}}_{1}},1/0 \right)}+{{m}_{2}}\overrightarrow{\Gamma \left( {{\text{O}}_{\text{2}}},2/0 \right)}+{{m}_{3}}\overrightarrow{\Gamma \left( {{\text{G}}_{\text{3}}},3/0 \right)}\)
avec
\(\overrightarrow{\Gamma \left( {{\text{O}}_{1}},1/0 \right)}=\overrightarrow{0}\) car O1 fixe dans le mouvement de 1/0 (il appartient à l’axe de rotation et z constant)
\(\overrightarrow{\Gamma \left( {{\text{O}}_{\text{2}}},2/0 \right)}=\left( \ddot{x}-\left( d+x \right){{{\dot{\psi }}}^{2}} \right)\overrightarrow{{{x}_{1}}}+\left( 2\dot{x}\dot{\psi }+\left( d+x \right)\ddot{\psi } \right)\overrightarrow{{{y}_{1}}}\) (calculée précédemment)
\(\overrightarrow{\Gamma ({{\text{G}}_{\text{3}}},3/0)}=-d{{\dot{\psi }}^{2}}\overrightarrow{{{x}_{1}}}+d\ddot{\psi }\overrightarrow{{{y}_{1}}}-l{{\left( \dot{\theta }+\dot{\psi } \right)}^{2}}\overrightarrow{{{x}_{3}}}+l\left( \ddot{\theta }+\ddot{\psi } \right)\overrightarrow{{{y}_{3}}}\) (donnée dans l’énoncé)
Le théorème de la résultante dynamique appliqué à \(S\) en projection sur l'axe \(\overrightarrow{{{z}_{0,1,3}}}\) permet d’écrire :
\({{Z}_{02}}-\left( {{m}_{1}}+{{m}_{2}}+{{m}_{3}} \right)g=0 \quad (8)\)
Le moment dynamique de l’ensemble \(S\) au point \({{\text{O}}_{\text{1}}}\) est égal à la somme des moments dynamiques, au même point, des éléments qui le composent :
\(\overrightarrow{\delta \left( {{\text{O}}_{\text{1}}},S/0 \right)}=\overrightarrow{\delta \left( {{\text{O}}_{\text{1}}},1/0 \right)}+\overrightarrow{\delta \left( {{\text{O}}_{\text{1}}},2/0 \right)}+\overrightarrow{\delta \left( {{\text{O}}_{\text{1}}},3/0 \right)}\)
Avec \(\overrightarrow{\delta \left( {{\text{O}}_{\text{1}}},1/0 \right)}=\frac{d}{dt}{{\left( \overline{\overline{{{I}_{{{\text{O}}_{\text{1}}},1}}}}.\overrightarrow{{{\Omega }_{1/0}}} \right)}_{{{R}_{0}}}}={{C}_{1}}\ddot{\psi }\overrightarrow{{{z}_{0}}}\)
On connaît le moment dynamique de la roue (2) en son centre d’inertie \({{\text{O}}_{\text{2}}}\)
\(\overrightarrow{\delta ({{\text{O}}_{\text{2}}},2/0)}={{A}_{2}}\ddot{\phi }\overrightarrow{{{x}_{1}}}+\left( {{A}_{2}}-{{B}_{2}} \right)\dot{\psi }\dot{\phi }\overrightarrow{{{y}_{1}}}+{{B}_{2}}\ddot{\psi }\overrightarrow{{{z}_{1}}}\)
On le transporte donc en \({{\text{O}}_{\text{1}}}\)
\(\begin{align} & \overrightarrow{\delta ({{\text{O}}_{\text{1}}},2/0)}=\overrightarrow{\delta ({{\text{O}}_{\text{2}}},2/0)}+\overrightarrow{{{\text{O}}_{\text{1}}}{{\text{O}}_{\text{2}}}}\wedge {{m}_{2}}\overrightarrow{\Gamma ({{\text{O}}_{\text{2}}},2/0)} \\ & ={{\left( \begin{matrix} {{A}_{2}}\ddot{\phi } \\ {{A}_{2}}\dot{\psi }\dot{\phi } \\ {{B}_{2}}\ddot{\psi } \\ \end{matrix} \right)}_{{{R}_{1}}}}+{{\left( \begin{matrix} d+x \\ 0 \\ 0 \\ \end{matrix} \right)}_{{{R}_{1}}}}\wedge {{m}_{2}}{{\left( \begin{matrix} \ddot{x}-\left( d+x \right){{{\dot{\psi }}}^{2}} \\ 2\dot{x}\dot{\psi }+\left( d+x \right)\ddot{\psi } \\ 0 \\ \end{matrix} \right)}_{{{R}_{1}}}} \\ & ={{\left( \begin{matrix} {{A}_{2}}\ddot{\phi } \\ {{A}_{2}}\dot{\psi }\dot{\phi } \\ {{B}_{2}}\ddot{\psi }+2{{m}_{2}}\left( d+x \right)\dot{x}\dot{\psi }+{{m}_{2}}{{\left( d+x \right)}^{2}}\ddot{\psi } \\ \end{matrix} \right)}_{{{R}_{1}}}} \end{align}\)
On a déjà calculé :
\(\overrightarrow{\delta \left( {{\text{O}}_{\text{3}}},3/0 \right)}={{m}_{3}}l\left[ d\left( {{{\dot{\psi }}}^{2}}sin\theta +\ddot{\psi }cos\theta \right)+l\left( \ddot{\theta }+\ddot{\psi } \right) \right]\overrightarrow{{{z}_{3}}}\)
\(\begin{align} & \overrightarrow{\delta \left( {{\text{O}}_{\text{1}}},3/0 \right)}=\overrightarrow{\delta \left( {{\text{O}}_{\text{3}}},3/0 \right)}+\overrightarrow{{{\text{O}}_{\text{1}}}{{\text{O}}_{\text{3}}}}\wedge {{m}_{3}}\overrightarrow{\Gamma ({{\text{G}}_{\text{3}}},3/0)} \\ & ={{m}_{3}}l\left[ d\left( {{{\dot{\psi }}}^{2}}sin\theta +\ddot{\psi }cos\theta \right)+l\left( \ddot{\theta }+\ddot{\psi } \right) \right]\overrightarrow{{{z}_{1,3}}} \\ & +{{\left( \begin{matrix} d \\ 0 \\ h \\\end{matrix} \right)}_{{{R}_{1}}}}\wedge {{m}_{3}}{{\left( \begin{array}{*{35}{l}} -d{{{\dot{\psi }}}^{2}}-l{{\left( \dot{\theta }+\dot{\psi } \right)}^{2}}\cos \theta -l\left( \ddot{\theta }+\ddot{\psi } \right)\sin \theta \\ d\ddot{\psi }-l{{\left( \dot{\theta }+\dot{\psi } \right)}^{2}}\sin \theta +l\left( \ddot{\theta }+\ddot{\psi } \right)\cos \theta \\ 0 \\\end{array} \right)}_{{{R}_{1}}}} \end{align}\)
\(\begin{align} & \overrightarrow{\delta \left( {{\text{O}}_{\text{1}}},3/0 \right)}.\overrightarrow{{{z}_{\text{0,1,3}}}}={{m}_{3}}l\left[ d\left( {{{\dot{\psi }}}^{2}}sin\theta +\ddot{\psi }cos\theta \right)+l\left( \ddot{\theta }+\ddot{\psi } \right) \right]+{{m}_{3}}d\left( d\ddot{\psi }-l{{\left( \dot{\theta }+\dot{\psi } \right)}^{2}}\sin \theta +l\left( \ddot{\theta }+\ddot{\psi } \right)\cos \theta \right) \\ & ={{m}_{3}}\left( \left( {{d}^{2}}+{{l}^{2}}+2dlcos\theta \right)\ddot{\psi }+\left( {{l}^{2}}+dl\cos \theta \right)\ddot{\theta }-dl{{\left( \dot{\theta }+\dot{\psi } \right)}^{2}}\sin \theta +dl{{{\dot{\psi }}}^{2}}sin\theta \right) \end{align}\)
Le théorème du moment dynamique appliqué à \(S\) au point \({{\text{O}}_{\text{1}}}\) en projection sur l'axe \(\overrightarrow{{{z}_{0,1,3}}}\) s’écrit :
\(\begin{align} & \left( d+x \right){{Y}_{02}}+{{C}_{m}}=\left[ {{C}_{1}}+{{B}_{2}}+{{m}_{2}}{{\left( d+x \right)}^{2}}+{{m}_{3}}\left( {{d}^{2}}+2dlcos\theta +{{l}^{2}} \right) \right]\ddot{\psi } \\ & +2{{m}_{2}}\left( d+x \right)\dot{x}\dot{\psi }-{{m}_{3}}dlsin\theta {{{\dot{\theta }}}^{2}}-2{{m}_{3}}dlsin\theta \dot{\theta }\dot{\psi }+{{m}_{3}}l\left( dcos\theta +l \right)\ddot{\theta } \end{align} \quad (9)\)
Bilan : système d’équations
\((1) \quad \Rightarrow \quad z=R=cte\)
\((2) \quad \Rightarrow \quad \left( d+x \right)\dot{\psi }+R\dot{\phi }=0\)
\((3) \quad \Rightarrow \quad \overrightarrow{{{F}_{res/2}}}={{F}_{res}}\overrightarrow{{{x}_{1}}}=-kx\overrightarrow{{{x}_{1}}}\)
\((4) \quad \Rightarrow \quad \overrightarrow{{{F}_{0/2}}}.\overrightarrow{{{x}_{1}}}={{X}_{02}}=-Darctan\left( \frac{{\dot{x}}}{\left( d+x \right)\dot{\psi }} \right)\)
\((5) \quad \Rightarrow \quad C_{m}^{'}={{m}_{3}}l\left[ d\left( {{{\dot{\psi }}}^{2}}sin\theta +\ddot{\psi }cos\theta \right)+l\left( \ddot{\theta }+\ddot{\psi } \right) \right]\)
\((6)+(3)+(4) \quad \Rightarrow \quad kx+Darctan\left( \frac{{\dot{x}}}{\left( d+x \right)\dot{\psi }} \right)+{{m}_{2}}\left[ \ddot{x}-\left( d+x \right){{{\dot{\psi }}}^{2}} \right]=0 \quad (10)\)
\((7) \quad \Rightarrow \quad {{Y}_{02}}=\frac{{{A}_{2}}}{R}\ddot{\phi }\)
\((8) \quad \Rightarrow \quad {{Z}_{02}}=\left( {{m}_{1}}+{{m}_{2}}+{{m}_{3}} \right)g\)
\((9)+(7) \quad \Rightarrow \quad \begin{array}{*{35}{l}} {{C}_{m}}=\left[ \left( {{C}_{1}}+{{B}_{2}} \right)+{{m}_{2}}{{\left( d+x \right)}^{2}}+{{m}_{3}}\left( {{d}^{2}}+2dlcos\theta +{{l}^{2}} \right) \right]\ddot{\psi }-\left( d+x \right)\frac{{{A}_{2}}}{R}\ddot{\phi } \\ +{{m}_{3}}l\left( dcos\theta +l \right)\ddot{\theta }+2{{m}_{2}}\left( d+x \right)\dot{x}\dot{\psi }-{{m}_{3}}dlsin\theta {{{\dot{\theta }}}^{2}}-2{{m}_{3}}dlsin\theta \dot{\theta }\dot{\psi } \\\end{array} \quad (11)\)
La résolution des équations différentielles \((2), (5), (10)\) et \((11)\) permet de déterminer les paramètres cinématiques \(x, \psi , \phi\) et \(\theta\) (le paramètre \(z\) étant déjà déterminé grâce à l'équation \((1)\)).
Etude de l’état stationnaire
Défini par :
\(x=cte={{x}^{*}}\) \(\dot{\psi }=cte=\omega\) \(\dot{\phi }=cte=\Omega\) \(\dot{\theta }=cte={{\dot{\theta }}^{*}}\)
Question
Trouver les couples moteurs et \({{x}^{*}}\) pour cet état stationnaire.
Solution
Dans le cas de l'état stationnaire définit dans l'énoncé :
\(x=cte={{x}^{*}}\) ; \(\dot{\psi }=cte=\omega\) ; \(\dot{\phi }=cte=\Omega\) ; \(\dot{\theta }=cte={{\dot{\theta }}^{*}}\)
Le système d'équations précédent devient (seules les équations qui diffèrent ont été écrites) :
\((2) \quad \Rightarrow \quad \left( d+{{x}^{*}} \right)\omega +R\Omega =0 \quad (12)\)
\((3) \quad \Rightarrow \quad {{F}_{R}}=-k{{x}^{*}} \quad (13)\)
\((4) \quad \Rightarrow \quad {{X}_{02}}=0 \quad (14)\)
\((5) \quad \Rightarrow \quad C_{m}^{'}={{m}_{3}}ld{{\omega }^{2}}sin\theta \quad (15)\)
\((10) \quad \Rightarrow \quad \left( k-{{m}_{2}}{{\omega }^{2}} \right){{x}^{*}}={{m}_{2}}{{\omega }^{2}}d$$\Rightarrow \quad {{x}^{*}}=\frac{{{m}_{2}}{{\omega }^{2}}d}{k-{{m}_{2}}{{\omega }^{2}}} \quad (16)\)
\((7) \quad \Rightarrow \quad {{Y}_{02}}=0 \quad (17)\)
\((11) \quad \Rightarrow \quad {{C}_{m}}=-{{m}_{3}}dlsin\theta {{\dot{\theta }}^{*}}\left( {{{\dot{\theta }}}^{*}}+2\omega \right) \quad (18)\)
Les équations \((15), (16)\) et \((18)\) permettent de déterminer les couples moteurs et \({{x}^{*}}.\)
Question
On propose de donner la condition de stabilité des petits mouvements axiaux de la roue au voisinage de l’état stationnaire. On fait l’hypothèse que \(\dot{\psi }=cte=\omega\) et on pose : \(x={{x}^{*}}+\bar{x}\) avec \(\bar{x}\) ainsi que \(\dot{\bar{x}}\) et \(\ddot{\bar{x}}\) petits.
Ecrire l’équation linéarisée caractérisant les petits mouvements axiaux de la roue.
Traduire la condition de stabilité qui, dans le cas d’une équation différentielle du second ordre à coefficients constants, est que tous les coefficients soient du même signe.
Solution
L'équation \((10)\) caractérisant les mouvements axiaux de la roue peut être linéarisée dans le cadre de l'hypothèse de petits mouvements autour de l’état stationnaire.
\(x={{x}^{*}}+\bar{x}\)
Le développement limité de la fonction arctan en 0 permet d’écrire :
\(arctan\left( \frac{{\dot{\bar{x}}}}{\left( d+{{x}^{*}}+\bar{x} \right)\omega } \right)\approx \frac{{\dot{\bar{x}}}}{\left( d+{{x}^{*}} \right)\omega }\)
L'équation \((10)\) devient : \({{m}_{2}}\ddot{\bar{x}}+\frac{D}{\left( d+{{x}^{*}} \right)\omega }\dot{\bar{x}}+\left( k-{{m}_{2}}{{\omega }^{2}} \right)\bar{x}={{m}_{2}}\left( d+{{x}^{*}} \right){{\omega }^{2}}-k{{x}^{*}} \quad (19)\)
En introduisant l'équation \((16)\) dans l'équation \((19)\), on obtient :
\(\ddot{\bar{x}}+\frac{\left( k-{{m}_{2}}{{\omega }^{2}} \right)D}{{{m}_{2}}kd\omega }\dot{\bar{x}}+\left( \frac{k}{{{m}_{2}}}-{{\omega }^{2}} \right)\bar{x}=0 \quad (20)\)
Le système est stable si tous les coefficients sont de même signe, soit : \(\omega <\sqrt{\frac{k}{{{m}_{2}}}}\quad (21)\)
Question
Déterminer les actions de la liaison L1-3 à l’état stationnaire.
Solution
Actions de la liaison 1-3 à l'état stationnaire
Pour déterminer les actions de la liaison 1-3, on isole l’ensemble des solides situés « après » la liaison 1-3 : donc le solide S3.
Bilan des AME (Actions Mécaniques Extérieures) sur le solide 3
Action de pesanteur : \({{\left\{ {{\Im }_{pes/3}} \right\}}_{{{O}_{3}}}}=\left\{ \begin{matrix} -{{m}_{3}}g\overrightarrow{{{z}_{0,1,3}}} \\ {{m}_{3}}gl\overrightarrow{{{y}_{3}}} \\\end{matrix} \right\}\)
Liaison 1/3 : \({{\left\{ {{\Im }_{1/3}} \right\}}_{{{O}_{3}}}}=\left\{ \begin{matrix} {{X}_{13}}\overrightarrow{{{x}_{3}}}+{{Y}_{13}}\overrightarrow{{{y}_{3}}}+{{Z}_{13}}\overrightarrow{{{z}_{1,3}}} \\ {{L}_{13}}\overrightarrow{{{x}_{3}}}+{{M}_{13}}\overrightarrow{{{y}_{3}}} \\ \end{matrix} \right\}\)
Couple moteur : \(\left\{ {{\Im }_{m'/3}} \right\}=\left\{ \begin{matrix} \overrightarrow{0} \\ {{C}_{m'}}\overrightarrow{{{z}_{0,1,3}}} \\\end{matrix} \right\}\)
Résultante et moment dynamique (calculé précédemment) à l’état stationnaire
\(\overrightarrow{D_{3/0}^{{}}}=-{{m}_{3}}\left[ d{{\omega }^{2}}\cos \theta +l{{\left( {{{\dot{\theta }}}^{*}}+\omega \right)}^{2}} \right]\overrightarrow{{{x}_{3}}}+{{m}_{3}}d{{\omega }^{2}}\sin \theta \overrightarrow{{{y}_{3}}}\)
\(\overrightarrow{\delta \left( {{\text{O}}_{3}},3/0 \right)}={{m}_{3}}ld{{\omega }^{2}}sin\theta \overrightarrow{{{z}_{1,3}}}\)
PFD à S3 au point O3
En projection dans \({{R}_{3}}\).
\({{X}_{13}}=-{{m}_{3}}\left[ d{{\omega }^{2}}\cos \theta +l{{\left( {{{\dot{\theta }}}^{*}}+\omega \right)}^{2}} \right] \quad (22)\) | \({{L}_{13}}=0 \quad (23)\) |
\({{Y}_{13}}={{m}_{3}}d{{\omega }^{2}}sin\theta \quad (24)\) | \({{M}_{13}}=-{{m}_{3}}gl \quad (25)\) |
\({{Z}_{13}}={{m}_{3}}g \quad (26)\) | \({{C}_{m'}}={{m}_{3}}ld{{\omega }^{2}}sin\theta \quad (15)\) |
Complément : Autre solution (plus complexe)
Si action 13 exprimée dans \({{R}_{1}}.\)
Bilan des AME (Actions Mécaniques Extérieures)
\({{\left\{ {{\Im }_{pes/3}} \right\}}_{{{O}_{3}}}}=\left\{ \begin{matrix} -{{m}_{3}}g\overrightarrow{{{z}_{0,1}}} \\ -{{m}_{3}}glsin\theta \overrightarrow{{{x}_{1}}}+{{m}_{3}}glcos\theta \overrightarrow{{{y}_{1}}} \\ \end{matrix} \right\}$${{\left\{ {{\Im }_{1/3}} \right\}}_{{{O}_{3}}}}=\left\{ \begin{matrix} {{X}_{13}}\overrightarrow{{{x}_{1}}}+{{Y}_{13}}\overrightarrow{{{y}_{1}}}+{{Z}_{13}}\overrightarrow{{{z}_{1}}} \\ {{L}_{13}}\overrightarrow{{{x}_{1}}}+{{M}_{13}}\overrightarrow{{{y}_{1}}} \\ \end{matrix} \right\}$ $\left\{ {{\Im }_{m'/3}} \right\}=\left\{ \begin{matrix} \overrightarrow{0} \\ {{C}_{m'}}\overrightarrow{{{z}_{0,1}}} \\\end{matrix} \right\}\)
Résultante et moment dynamique :
\(\overrightarrow{D_{3/0}^{{}}}=-{{m}_{3}}\left[ d{{\omega }^{2}}+l{{\left( {{{\dot{\theta }}}^{*}}+\omega \right)}^{2}}cos\theta \right]\overrightarrow{{{x}_{1}}}-{{m}_{3}}l{{\left( {{{\dot{\theta }}}^{*}}+\omega \right)}^{2}}sin\theta \overrightarrow{{{y}_{1}}}\)
\(\overrightarrow{\delta \left( {{\text{O}}_{3}},3/0 \right)}={{m}_{3}}ld{{\omega }^{2}}sin\theta \overrightarrow{{{z}_{1,3}}}\)
En appliquant le PFD à S3 au point O3 en projection dans \({{R}_{1}},\) on obtient :
\({{X}_{13}}=-{{m}_{3}}\left[ d{{\omega }^{2}}+l{{\left( {{{\dot{\theta }}}^{*}}+\omega \right)}^{2}}cos\theta \right] \quad (27)\) | \({{L}_{13}}={{m}_{3}}glsin\theta \quad (28)\) |
\({{Y}_{13}}=-{{m}_{3}}l{{\left( {{{\dot{\theta }}}^{*}}+\omega \right)}^{2}}sin\theta \quad (29)\) | \({{M}_{13}}=-{{m}_{3}}glcos\theta \quad (30)\) |
\({{Z}_{13}}={{m}_{3}}g \quad (31)\) | \({{C}_{m'}}={{m}_{3}}ld{{\omega }^{2}}sin\theta \quad (15)\) |
Application du théorème de l’énergie cinétique à l’ensemble
\(\)
Question
Calculer la puissance galiléenne développée par toutes les actions mécaniques.
Calculer l’énergie cinétique galiléenne.
Appliquer le théorème de l’énergie cinétique à l’état stationnaire.
Solution
Puissance des actions mécaniques
La puissance développée par les actions mécaniques intérieures au système est :
\({{P}_{\operatorname{int}}}=P_{li12}^{{}}+P_{li13}^{{}}+P_{ressort}^{{}}+P_{m'}^{{}}\)
Les liaisons intérieures (1/2 et 1/3) sont parfaites : elles ne développent donc pas de puissance.
\(\Rightarrow \quad P_{li01}^{{}}=0,\ P_{li12}^{{}}=0\ et\ P_{li13}^{{}}=0\)
La puissance développée par le ressort est : \(P_{ressort}^{{}}=-k\left( l-{{l}_{0}} \right)\frac{dl}{dt}=-kx\dot{x}\)
La puissance développée par le moteur entre 1 et 3 est : \(P_{m'}^{0}=\overrightarrow{{{M}_{m'\to 1}}\left( {{\text{O}}_{\text{3}}} \right)}.\overrightarrow{\Omega _{3/1}^{{}}}={{C}_{m'}}\dot{\theta }\)
La puissance galiléenne développée par les actions mécaniques extérieures s’exerçant sur le système est :
\({{P}_{ext/0}}=P_{0\to 1/0}^{{}}+P_{0\to 2/0}^{{}}+P_{m/0}^{{}}\)
\(P_{0\to 1/0}^{{}}=0\) car la liaison est parfaite et le déplacement suivant \(z\) est nul (hypothèse de contact permanent).
De même l’action de pesanteur ne travaille pas (altitude constante).
\(P_{0\to 2/0}^{{}}=\overrightarrow{{{F}_{0\to 2}}}.\overrightarrow{V\left( \text{I},2/0 \right)}={{X}_{02}}\dot{x}+{{Y}_{02}}\left[ \left( d+x \right)\dot{\psi }+R\dot{\phi } \right]={{X}_{02}}\dot{x}\) (en utilisant l'équation de liaison)
\(P_{m/0}^{{}}=\overrightarrow{{{M}_{m\to 1}}\left( {{\text{O}}_{1}} \right)}.\overrightarrow{\Omega _{1/0}^{{}}}={{C}_{m}}\dot{\psi }\)
La puissance développée par le système est donc :
\({{P}_{\operatorname{int}}}+{{P}_{ext/0}}=\left( {{X}_{02}}-kx \right)\dot{x}+{{C}_{m}}\dot{\psi }+{{C}_{m'}}\dot{\theta }\)
Energie cinétique
L'énergie cinétique du système est la somme des énergies cinétiques des solides qui le composent.
\({{T}_{S/0}}=T_{1/0}^{{}}+T_{2/0}^{{}}+T_{3/0}^{{}}$ avec $T_{i/0}^{{}}=\frac{1}{2}{{m}_{i}}\overrightarrow{V\left( {{\text{G}}_{i}},i/0 \right)}+\frac{1}{2}{{\overrightarrow{\Omega _{i/0}^{{}}}}^{t}}.\overline{\overline{{{I}_{{{G}_{i}},i}}}}.\overrightarrow{\Omega _{i/0}^{{}}}\)
avec \(T_{1/0}^{{}}=\frac{1}{2}{{C}_{1}}{{\dot{\psi }}^{2}}\)
\(T_{2/0}^{{}}=\frac{1}{2}{{m}_{2}}\left[ {{{\dot{x}}}^{2}}+{{\left( d+x \right)}^{2}}{{{\dot{\psi }}}^{2}} \right]+\frac{1}{2}\left( {{A}_{2}}{{{\dot{\phi }}}^{2}}+{{B}_{2}}{{{\dot{\psi }}}^{2}} \right)\)
\(T_{3/0}^{{}}=\frac{1}{2}{{m}_{3}}\left[ {{d}^{2}}{{{\dot{\psi }}}^{2}}+2dl\dot{\psi }\left( \dot{\theta }+\dot{\psi } \right)cos\theta +{{l}^{2}}{{\left( \dot{\theta }+\dot{\psi } \right)}^{2}} \right]\)
L'énergie cinétique du système est donc :
\(\begin{align} & T=\frac{1}{2}\left[ {{C}_{1}}+{{B}_{2}}+{{m}_{2}}{{\left( d+x \right)}^{2}}+{{m}_{3}}\left( {{d}^{2}}+{{l}^{2}}+2dlcos\theta \right) \right]{{{\dot{\psi }}}^{2}} \\ & \quad +\frac{1}{2}{{A}_{2}}{{{\dot{\phi }}}^{2}}+\frac{1}{2}{{m}_{3}}{{l}^{2}}{{{\dot{\theta }}}^{2}}+\frac{1}{2}{{m}_{2}}{{{\dot{x}}}^{2}}+{{m}_{3}}l\left( l+dcos\theta \right)\dot{\theta }\dot{\psi } \end{align}\)
\(\overrightarrow{V\left( {{\text{G}}_{3}}/0 \right)}={{\left. \frac{d\overrightarrow{\text{O}{{\text{G}}_{\text{3}}}}}{dt} \right|}_{0}}={{\left. \frac{d\overrightarrow{\text{O}{{\text{O}}_{3}}}+\overrightarrow{{{\text{O}}_{\text{3}}}{{\text{G}}_{\text{3}}}}}{dt} \right|}_{0}}={{\left. \frac{d}{dt}\left( d\overrightarrow{{{x}_{1}}}+h\overrightarrow{z} \right) \right|}_{0}}+{{\left. \frac{d}{dt}l\overrightarrow{{{x}_{3}}} \right|}_{0}}=d\dot{\psi }\overrightarrow{{{y}_{1}}}+l\left( \dot{\psi }+\dot{\theta } \right)\overrightarrow{{{y}_{3}}}\)
Application du théorème de l'énergie cinétique
La dérivée de l'énergie cinétique par rapport au temps est :
\(\begin{align} & \frac{d{{T}_{S/0}}}{dt}=\left[ {{C}_{1}}+{{B}_{2}}+{{m}_{2}}{{\left( d+x \right)}^{2}}+{{m}_{3}}\left( {{d}^{2}}+{{l}^{2}}+2dlcos\theta \right) \right]\dot{\psi }\ddot{\psi }+\left( {{m}_{2}}x\dot{x}-{{m}_{3}}dlsin\theta \dot{\theta } \right){{{\dot{\psi }}}^{2}} \\ & +{{A}_{2}}\dot{\phi }\ddot{\phi }+{{m}_{3}}{{l}^{2}}\dot{\theta }\ddot{\theta }+{{m}_{2}}\dot{x}\ddot{x}-{{m}_{3}}ldsin\theta {{{\dot{\theta }}}^{2}}\dot{\psi }+{{m}_{3}}l\left( l+dcos\theta \right)\left( \ddot{\theta }\dot{\psi }+\dot{\theta }\ddot{\psi } \right) \end{align}\)
A l’état stationnaire :
\(\frac{d{{T}_{S/0}}}{dt}=-{{m}_{3}}dlsin\theta \left( {{{\dot{\theta }}}^{*}}{{\omega }^{2}}+{{{\dot{\theta }}}^{*2}}\omega \right)\)
Le théorème de l'énergie cinétique à l'état stationnaire donne, en utilisant l'équation \({{X}_{02}}=0\) :
\(-{{m}_{3}}dlsin\theta \left( {{{\dot{\theta }}}^{*}}{{\omega }^{2}}+{{{\dot{\theta }}}^{*2}}\omega \right)={{C}_{m}}\omega +{{C}_{m'}}{{\dot{\theta }}^{*}} \quad (32)\)
Remarque :
On peut vérifier l'équation \((32)\) en utilisant les équations \((15)\) et \((18)\).