Fonction de force d’un ressort
Ressort de traction/compression
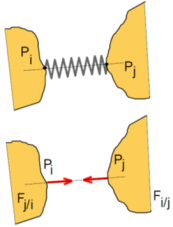
Pour un ressort de traction/compression de raideur \(k\) [N/m] et de longueur à vide \({l_0}\) ancrer au solide \({S_i}\) en un point \({{\rm{P}}_i}\) et au solide \({S_j}\) en \({{\rm{P}}_j},\) le solide \({S_i}\) agit sur le solide \({S_j}\) sous la forme d’un glisseur dont la résultante est :
\(\overrightarrow {{F_{i \to j}}} = - k\left( {l - {l_0}} \right)\overrightarrow u = - \overrightarrow {{F_{j \to i}}}\)
avec \(\overrightarrow u = \frac{{\overrightarrow {{{\rm{P}}_i}{{\rm{P}}_j}} }}{{\left\| {\overrightarrow {{{\rm{P}}_i}{{\rm{P}}_j}} } \right\|}} = \frac{{\overrightarrow {{{\rm{P}}_i}{{\rm{P}}_j}} }}{l} = \frac{{\left( {x - {x_{{{\rm{P}}_i}}}} \right)\overrightarrow {{x_g}} + \left( {y - {y_{{{\rm{P}}_i}}}} \right)\overrightarrow {{y_g}} + \left( {z - {z_{{{\rm{P}}_i}}}} \right)\overrightarrow {{z_g}} }}{{\sqrt {{{\left( {x - {x_{{{\rm{P}}_i}}}} \right)}^2} + {{\left( {y - {y_{{{\rm{P}}_i}}}} \right)}^2} + {{\left( {z - {z_{{{\rm{P}}_i}}}} \right)}^2}} }}\)
\(\begin{array}{l} \overrightarrow {{F_{i \to j}}} .\overrightarrow {{x_g}} = - k\left( {l - {l_0}} \right)\frac{{x - {x_{{{\rm{P}}_i}}}}}{l} = - k\left( {l - {l_0}} \right)\frac{{\partial l}}{{\partial x}} = \frac{{\partial {U_r}}}{{\partial x}}\\ \overrightarrow {{F_{i \to j}}} .\overrightarrow {{y_g}} = - k\left( {l - {l_0}} \right)\frac{{y - {y_{{{\rm{P}}_i}}}}}{l} = - k\left( {l - {l_0}} \right)\frac{{\partial l}}{{\partial y}} = \frac{{\partial {U_r}}}{{\partial y}}\\ \overrightarrow {{F_{i \to j}}} .\overrightarrow {{z_g}} = - k\left( {l - {l_0}} \right)\frac{{z - {z_{{{\rm{P}}_j}}}}}{l} = - k\left( {l - {l_0}} \right)\frac{{\partial l}}{{\partial z}} = \frac{{\partial {U_r}}}{{\partial z}} \end{array}\)
Donc \({U_r} = - \frac{1}{2}k{\left( {l - {l_0}} \right)^2} + cte\)
\(\begin{array}{c} {P_{ressort\;i \to j}} = \overrightarrow {{F_{i \to j}}} .\overrightarrow {V({{\rm{P}}_j}/g)} = - k\left( {l - {l_0}} \right)\overrightarrow u .\frac{d}{{dt}}{\left( {\overrightarrow {{O_g}{{\rm{P}}_i}} + l\overrightarrow u } \right)_g}\\ = - k\left( {l - {l_0}} \right)\overrightarrow u .\left( {\frac{{dl}}{{dt}}\overrightarrow u + l{{\left. {\frac{{d\overrightarrow u }}{{dt}}} \right|}_g}} \right)\quad si\;{P_i}\;fixe\;dans\;{R_g}\\ = - k\left( {l - {l_0}} \right)\frac{{dl}}{{dt}}\quad {\rm{car}}\quad \overrightarrow u .{\left. {\frac{{d\overrightarrow u }}{{dt}}} \right|_g} = 0 \end{array}\)
On sait que \({P_{ressort\;i \to j}} = \frac{{d{U_r}}}{{dt}}\) d’où \(d{U_r} = - k\left( {l - {l_0}} \right)dl\) donc \({U_r} = - \frac{1}{2}k{\left( {l - {l_0}} \right)^2} + cte\).
Cas où le ressort est intérieur au système isolé
\(\begin{array}{c} {P_{ressort}} = \overrightarrow {{F_{i \to j}}} .\overrightarrow {V({{\rm{P}}_j}/g)} + \overrightarrow {{F_{j \to i}}} .\overrightarrow {V({{\rm{P}}_i}/g)} = \overrightarrow {{F_{i \to j}}} .\left( {\overrightarrow {V({{\rm{P}}_j}/g)} - \overrightarrow {V({{\rm{P}}_i}/g)} } \right)\\ = \overrightarrow {{F_{i \to j}}} .\left( {{{\left. {\frac{{d\overrightarrow {{{\rm{O}}_{\rm{g}}}{{\rm{P}}_j}} }}{{dt}}} \right|}_g} - {{\left. {\frac{{d\overrightarrow {{{\rm{O}}_{\rm{g}}}{{\rm{P}}_i}} }}{{dt}}} \right|}_g}} \right) = \overrightarrow {{F_{i \to j}}} .{\left. {\frac{{d\overrightarrow {{{\rm{P}}_i}{{\rm{P}}_j}} }}{{dt}}} \right|_g} = \overrightarrow {{F_{i \to j}}} .{\left. {\frac{{d\left( {l\overrightarrow u } \right)}}{{dt}}} \right|_g} = - k\left( {l - {l_0}} \right)\frac{{dl}}{{dt}} \end{array}\)
On retrouve donc \({U_r} = - \frac{1}{2}k{\left( {l - {l_0}} \right)^2} + cte\).
Remarque :
Dans le cas où le ressort est intérieur au système, le principe d’action-réaction implique que la résultante des actions soit nulle \(\overrightarrow {{F_{i \to j}}} + \overrightarrow {{F_{j \to i}}} = \overrightarrow 0\) mais la puissance intérieure développée par le ressort n’est pas nulle.
Ressort de torsion
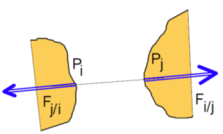
Pour un ressort de torsion de raideur \(k\) [N/rad] de position angulaire à vide \({\theta _0},\) le solide \({S_i}\) agit sur le solide \({S_j}\) sous la forme d’un couple dont le moment est :
\(\overrightarrow {{M_{i \to j}}({{\rm{P}}_j})} = - k\left( {\theta - {\theta _0}} \right)\overrightarrow u = - \overrightarrow {{M_{j \to i}}({{\rm{P}}_j})}\)
où \(\overrightarrow u = \frac{{\overrightarrow {{{\rm{P}}_i}{{\rm{P}}_j}} }}{l}\) est la direction de l’axe de rotation.
\(\begin{array}{c} {P_{ressort}} = \overrightarrow {{M_{i \to j}}({{\rm{P}}_j})} .\overrightarrow {{\Omega _{j/i}}} \\ = - k\left( {\theta - {\theta _0}} \right)\overrightarrow u .\dot \theta \overrightarrow u \\ = - k\left( {\theta - {\theta _0}} \right)\dot \theta \\ = \frac{{d{U_r}}}{{dt}} \end{array}\)
On en déduit que \({U_r} = - \frac{1}{2}k{\left( {\theta - {\theta _0}} \right)^2} + cte\)