Application PFS
Pour déterminer analytiquement l’équilibre statique d’un solide, il faut d’abord vérifier que l’on dispose d’autant d’équations que d’inconnues. Pour cela, on isole le solide et on fait le bilan des actions mécaniques qui s’appliquent sur lui (actions de liaison, pesanteur, pression, …). Chaque action mécanique peut introduire jusqu’à 6 inconnues pour les systèmes spatiaux (voir forme des torseurs d’action des liaisons normalisées) et jusqu’à 3 inconnues pour les modèles plans.
Pour un solide, on dispose de 6 équations (3 pour les modèles plans) pour déterminer ces inconnues. Si le nombre d’inconnues est égal au nombre d’équations alors on peut déterminer l’ensemble des inconnues.
Si le nombre d’inconnues est supérieur au nombre d’équations, le système est dit hyperstatique. Il faut alors trouver des équations supplémentaires pour résoudre comme des lois de comportement de déformations. Ce cas ne sera pas abordé dans le cadre du cours.
Pour un système à n solides, on ne peut isoler qu’un nombre de systèmes égal au nombre n de solides (pour obtenir des équations indépendantes). Chaque système (ou solide) fournit 6 équations (3 en plan), on a donc 6*n équations (ou 3*n en plan) pour déterminer autant d’inconnues.
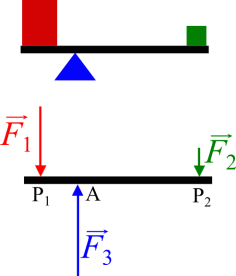
Soit un solide soumis à trois actions définies par les torseurs suivants :
\(\left\{ {{T_{1 \to S}}} \right\} = {\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {{F_1}} }\\{\overrightarrow 0 }\end{array}} \right\}_{{{\rm{P}}_1}}}\) \(\left\{ {{T_{2 \to S}}} \right\} = {\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {{F_2}} }\\{\overrightarrow 0 }\end{array}} \right\}_{{{\rm{P}}_2}}}\) \(\left\{ {{T_{3 \to S}}} \right\} = {\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {{F_3}} }\\{\overrightarrow 0 }\end{array}} \right\}_{\rm{A}}}\)
Le torseur équivalent à ces actions est :
\(\left\{ {{T_{1 + 2 + 3 \to S}}} \right\} = {\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} }\\{\overrightarrow {{\rm{A}}{{\rm{P}}{\rm{1}}}}\wedge \overrightarrow {{F_1}} + \overrightarrow {{\rm{A}}{{\rm{P}}{\rm{2}}}} \wedge \overrightarrow {{F_2}} }\end{array}} \right\}_{\rm{A}}}\)
Le solide est en équilibre statique si
\(\left\{ {{T_{1 + 2 + 3 \to S}}} \right\} = \left\{ 0 \right\}\quad \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow 0 }\\{\overrightarrow {{\rm{A}}{{\rm{P}}_{\rm{1}}}} \wedge \overrightarrow {{F_1}} + \overrightarrow {{\rm{A}}{{\rm{P}}_{\rm{2}}}} \wedge \overrightarrow {{F_2}} = \overrightarrow 0 }\end{array}} \right.\)