Renvoi d'angle
Le renvoi d’angle ci-dessous est composé de deux arbres portants des engrenages coniques.
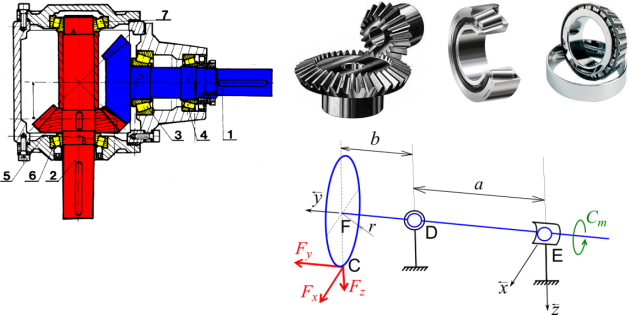
La modélisation de l’arbre moteur est donnée par le schéma ci-dessous.
Le torseur des actions de contact de 5/1 au point C est donné et a la forme suivante :
\(\left\{ {{T_{5 \to 1}}} \right\} = {\left\{ {\begin{array}{*{20}{c}} {{F_x}}&0\\ {{F_y}}&0\\ {{F_z}}&0 \end{array}} \right\}_C}\)
Le moteur entrainant l’arbre 1 tourne à vitesse constante. Il exerce un couple sur l’arbre 1 par l’intermédiaire d’un accouplement élastique :
\(\left\{ {{T_{m \to 1}}} \right\} = {\left\{ {\begin{array}{*{20}{c}} 0&0\\ 0&{{C_m}}\\ 0&0 \end{array}} \right\}_E}\)
Question
Donner l’expression du torseur des actions de contact 5/1 au point F.
Indice
Voir cours torseur.
Solution
\(\left\{ {{T_{5 \to 1}}} \right\} = {\left\{ {\begin{array}{*{20}{c}} {{F_x}}&0\\ {{F_y}}&0\\ {{F_z}}&0 \end{array}} \right\}_C} = {\left\{ {\begin{array}{*{20}{c}} {{F_x}}&{ - r{F_y}}\\ {{F_y}}&{r{F_x}}\\ {{F_z}}&0 \end{array}} \right\}_F} = {\left\{ {\begin{array}{*{20}{c}} {{F_x}}&{b{F_z} - r{F_y}}\\ {{F_y}}&{r{F_x}}\\ {{F_z}}&{ - b{F_x}} \end{array}} \right\}_D} = {\left\{ {\begin{array}{*{20}{c}} {{F_x}}&{(a + b){F_z} - r{F_y}}\\ {{F_y}}&{r{F_x}}\\ {{F_z}}&{ - (a + b){F_x}} \end{array}} \right\}_E}\)
Question
Donner la forme du torseur des actions mécaniques exercées par le carter sur l’arbre 1 en D et en E.
Solution
L’arbre 1 est en liaison rotule avec le carter par l’intermédiaire du roulement 3 :
\(\left\{ {{T_{3 \to 1}}} \right\} = {\left\{ {\begin{array}{*{20}{c}} {{F_{3x}}}&0\\ {{F_{3y}}}&0\\ {{F_{3z}}}&0 \end{array}} \right\}_D} = {\left\{ {\begin{array}{*{20}{c}} {{F_{3x}}}& {a{F_{3z}}}\\ {{F_{3y}}}&0\\ {{F_{3z}}}&{ - a{F_{3x}}} \end{array}} \right\}_E} = {\left\{ {\begin{array}{*{20}{c}} {{F_{3x}}}&{ - b{F_{3z}}}\\ {{F_{3y}}}&0\\ {{F_{3z}}}&{b{F_{3x}}} \end{array}} \right\}_F}\)
L’arbre 1 est en liaison linéaire annulaire avec le carter par l’intermédiaire du roulement 4 :
\(\left\{ {{T_{4 \to 1}}} \right\} = {\left\{ {\begin{array}{*{20}{c}} {{F_{4x}}}&0\\ 0&0\\ {{F_{4z}}}&0 \end{array}} \right\}_E} = {\left\{ {\begin{array}{*{20}{c}} {{F_{4x}}}&{ - a{F_{4z}}}\\ 0&0\\ {{F_{4z}}}&{a{F_{4x}}} \end{array}} \right\}_D} = {\left\{ {\begin{array}{*{20}{c}} {{F_{4x}}}&{ - (b + a){F_{4z}}}\\ 0&0\\ {{F_{4z}}}&{(b + a){F_{4x}}} \end{array}} \right\}_F}\)
Question
Déterminer, en écrivant l’équilibre de l’arbre, les actions exercées par le carter sur l’arbre 1 en D et E ainsi que le couple moteur en fonction de \({F_x},\) \({F_y},\) \({F_z},\) \(a,\) \(b\) et \(r.\)
Solution
L’action du couple moteur sur 1 est \(\left\{ {{T_{m \to 1}}} \right\} = {\left\{ {\begin{array}{*{20}{c}} 0&0\\ 0&{{C_m}}\\ 0&0 \end{array}} \right\}_E}\)